Критерий согласияПирсона
Критерий согласия Пирсона основан на определении в качестве меры расхождения U величины:
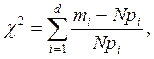
где mi – количество значений случайной величины η, попавших в i-й подынтервал; pi – вероятность попадания случайной величины η в i-й подынтервал, вычисленная из теоретического распределения; d – количество подынтервалов, на которые разбивается интервал измерения в компьютерном эксперименте.
При N→∞ закон распределения величины U, являющейся мерой расхождения, зависит только от числа подынтервалов и приближается к закону распределения χ2 (хи-квадрат) с (d–r–1) степенями свободы, где r – число параметров теоретического закона распределения.
Из теоремы Пирсона следует, что, какова бы ни была функция распределения F(у) случайной величины η, при N→∞ распределение величины χ2 имеет вид:
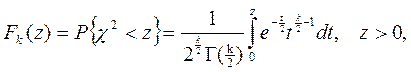
где Г(k/2) – гамма-функция; z – значение случайной величины χ2; k=d–r–1 – число степеней свободы. Функции распределения Fk(z) табулированы.
По вычисленному значению U=χ2 и числу степеней свободы k с помощью таблиц находится вероятность Р{ 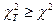 }. Если эта вероятность превышает некоторый уровень значимости γ, то считается, что гипотеза Н0 о виде распределения не опровергается результатами компьютерного эксперимента.
}. Если эта вероятность превышает некоторый уровень значимости γ, то считается, что гипотеза Н0 о виде распределения не опровергается результатами компьютерного эксперимента.
Дата добавления: 2021-09-07; просмотров: 522;











