Методи класифікації в ГІС

Визначення класів та об'єктів – одна з найскладніших задач у ГІС, хоча, зрозуміло апріорі, що одні класифікації можуть бути краще інших. Складність класифікації пояснюється двома важливими причинами.

По-перше, відсутнє визначення ”досконала класифікація”. Існує стільки способів поділу світу на об'єктні системи, скільки вчених розв’язує цю задачу: спосіб класифікації визначається метою, до якої ми прагнемо.

По-друге, розумна класифікація вимагає великої творчої енергії й проникливості. Іноді результат класифікації очевидний і тривіальний, іноді він справа смаку, а буває, що все залежить від уміння виділити головне. Це нагадує загадку: ”Чому лазерний промінь схожий на золотий ключик ”? – ”Тому, що ні той, ні інший не вміють свистіти”. Треба бути надзвичайно творчою людиною дослідником, щоб найти щось спільне в настільки незв’язаних предметах.

Істотні ознаки, що відповідають певним закономірностям певного класу не лежать на поверхні, а повинні бути знайдені за допомогою аналізу. Класифікація передбачає складний системний аналіз, змушує шукати змістовні ознаки. Цим підкреслюється, що розумна класифікація – робота інтелектуальна.

При нанесенні на карту кількісних показників з метою виявлення закономірностей розподілу об’єктів, завжди існує проблема вибору між поданням точних значень даних або узагальненням зазначених значень за площею. Зазвичай, зазначене число, кількість і відношення групуються в класи, тому що кожний об’єкт, як правило, має різні значення. Це особливо важливо враховувати, якщо діапазон значень великий. Якщо кожне значення представлене на карті унікальним символом і обране відображення точних значень об’єктів на карті, то оцінити ситуацію можна лише при невеликій кількості значень.

Класи дозволяють об’єднати об’єкти з подібними значеннями, при цьому приписуючи їм однаковий символ. Це дозволяє побачити розподіл об’єктів з подібними значеннями. Призначення діапазону класу покаже, які об’єкти, до якого класу будуть віднесені, що, в свою чергу, буде визначати зміст карти. Змінюючи класи, при однакових вихідних даних можна створювати різноманітні карти. Між об’єктами різних класів, як правило, вибирається максимальна відмінність значень, щоб забезпечити достатній контраст відображення і потрапляння об’єктів з подібними значеннями в один клас.

Класифікації можуть бути:

– простими (монокритеріальними), створеними на основі одного критерію (тип ландшафту);

– складними (багатокритеріальними) – на основі багатьох критеріїв (висота, кількість опадів, екологічні показники тощо).

Прості класифікації, як правило, використовуються для відображення безперервно змінюваних просторових властивостей, таких, як щільність населення, рівень забруднення повітряного басейну тощо, у вигляді легкодоступних карт хороплет[1] або картодіаграм. Класифікації підлягають не тільки дискретні об'єкти. Цілі напрямки моделювання й аналізу статистичних поверхонь, такі як побудова карт ухилів, експозиції, площ затоплення, зон видимості, буферних зон і смуг віддаленості, фактично є класифікацією.

Класифікації надзвичайно важливі для правильного сприйняття дійсності. Існують обмеження в можливій кількості класів, які без проблем може сприймати людина. Зазвичай, це 7±2 класи в ієрархічній системі. Класифікації з кількістю класів понад 10 є складними для сприйняття і роботи. Мала кількість діапазонів (менше 5-4) значною мірою узагальнює значення між сусідніми діапазонами, багато окремих груп значень можуть бути нівельованими.

Призначення класів у ГІС можна здійснити або вручну, або шляхом використання стандартних схем класифікації.

Призначення класів вручну.Ручну класифікацію застосовують лише тоді, коли необхідно згрупувати об’єкти, що відповідають специфічним критеріям, або порівняти значення їхніх атрибутів з конкретною характерною величиною.

Як у векторних, так і в растрових моделях, технологія класифікації об'єктів передбачає перекодування атрибутів в атрибутивних таблицях для створення нових покриттів. У цьому процесі класифікація спрямована на перейменування об'єктів на основі значень атрибутів, не змінюючи їх розташування. Визначається верхня йнижня межа інтервалу для кожного класу, а також приписується власний символ. Кожному діапазону присвоюється визначена графічна змінна залежно від типу картографічного об'єкта (точка, лінія або полігон). Графічні характеристики (тип, колір і розмір символу; колір, тип і товщина лінії; заповнення і колір полігона) вибираються з відповідних бібліотек, так само користувачу може бути запропонована певна кількість готових шаблонів оформлення карти.

Верхня чи нижня межа інтервалу класу може визначати певне явище. Наприклад, у разі необхідності позначення міської зони бідності потрібно відобразити райони, у яких не менше 35% населення живе нижче рівня бідності. У цьому випадку один клас визначив би на карті 35-відсоткову зону. Було б логічно призначити наступний інтервал для 50 %, показавши, _:у яких районах не менше половини населення живе за межею рівня бідності.

Класи можуть також ґрунтуватисяна прийнятих стандартах або результатах досліджень у будь-якій галузі господарства чи промисловості. Наприклад, біологи, створюючи заповідник, виключили б території річкових басейнів, покритих лісом менш ніж на 50 %, але виділили б ті, лісове покриття яких перевищує 85 %. У цьому випадку класи визначилися б як: ”менше 50%”, ”51 – 85%” і ”більше 85%”.

Можна також створювати класи, використовуючи узагальнюючі характеристики об'єктів. Припустимо, необхідно нанести на карту області середню для кожного району кількість людей, зайнятих усільському господарстві. Можна було б підібрати класи так, щоб один із них був обмежений середнім значенням даного параметра по всій країні. В цьому випадку карта б добре відображала відхилення локального показника від середнього по країні.

Треба відзначити, що зміна кодів атрибутів у ході ручної класифікації, – процес доволі прямолінійний, він іноді може створювати певні проблеми, головним чином унаслідок порядку, в якому змінюються числа. Особливо актуально цедля растрових відображень безперервних явищ, коли кожному пікселю може відповідати тільки одне значення, або в простих векторнихсистемах, які допускають класифікацію вже існуючого поля класів в атрибутивній таблиці.

Припустимо, наприклад, що об'єкти покриття з кодами атрибутів від 1 до 5 відповідають типам рослинності. Нехай класи 1,3 і 5 – лісові різновиди, а 2 і 4 – лугові. Потрібно створити карту тільки з двома категоріями: ліс (код 1) і луг (код 2).

У варіанті 1 (табл. 17.1) спочатку замінюємо класи 1, 3 і 5 на 1 (крок 1),а потім 2 і 4 – на 2 (крок 2). Змінивши легенду, отримуємо карту з лісами (1) ілугами (2).

Проаналізуємо, що відбувається, якщо новий клас ”1” призначити спочатку луговим елементам (варіант 2). У цьому випадку на першому кроці класи 2 і 4 одержать значення ”1”, і об'єкти знову утвореного класу ”1” зіллються з об'єктами, що мали попередньо клас ”1”. Таким чином, подальша класифікація вже буде з похибкою. Щоб уникнути подібних ситуацій, треба знати декілька корисних правил.

Таблиця 17.1.

По-перше, нові коди атрибутів не повинні зберігатися в одному покритті з вихідними. У крайньому випадку потрібно виокремити результати класифікації в окремий стовпчик атрибутивної таблиці.

По-друге, завжди стежте, яким чином перенумерація впливає на результат. Якщо виникають сумніви щодо порядку перенумерації, спробуйте виконати процесу зворотному порядку.

В ГІС з розвиненим аналітичним інструментарієм (ArcInfo, ArcView, System-9) функція класифікації зазвичай побудована таким чином, що нові класи призначаються обов'язково в новому полі атрибутивної таблиці, а при роботі з растровими даними класифікація призводить до створення нового покриття. Ці заходи виключають вплив порядку призначення класів на результат.

Використання стандартних схем класифікації.Зазвичай, коли метою класифікації даних є виявлення закономірностей просторового розподілу, використовуються стандартні схеми поділу даних на інтервали. Стандартні схеми враховують характер розподілу вибірки, при цьому автоматично визначаються інтервал поділу та кількість інтервалів.

Оптимальний вибір інтервалу розподілу, а також вірне визначення кількості класів допомагає зробити об'єктивний аналіз розподілу даних.

Для наочності карти дуже важливо, якими способами визначаються інтервали класифікації. Докладні дослідження в цій галузі проведені Евансом (Evans, 1977) [80], який запропонував класифікацію систем інтервалів.

Усі класифікаційні інтервали поділяються на екзогенні, умовні, ідеографічні та періодичні.

Екзогенні інтервали обирають згідно з граничними значеннями, що відносяться до наборів даних, але не випливають з них. Вони широко використовуються в класифікаціях ґрунтів й оцінці земель. Перевагами екзогенних інтервалів є те, що вони універсальні у використанні, а недоліками – те, що в деяких випадках вони не охоплюють усіх змін характеристики досліджуваного району.

Умовні інтервали мають нерегулярний характер, вибираються без якого будь-якого чіткого плану і часто навіть без попереднього аналізу даних. Якщо співвіднести їх з яким-небудь періодом часу, то утвориться екзогенна шкала інтервалів.

Ідеографічні інтервали вибираються з урахуванням специфічних аспектів набору даних. Вони включають методи розподілу даних на багатомодальні угруповування.

Періодичні інтервали мають межі, які знаходяться в прямому математичному зв'язку. Якщо ці межі обираються незалежно від характеристик окремого набору даних, то тоді отримувані за різними зразками або наборами даних результати є цілком порівнянні.

Програмне забезпечення ГІС підтримує різні методи класифікацій. Наприклад, ArcView пропонує п’ять методів класифікації:

– метод природних інтервалів – об’єкти поділяються на класи, серед наборів об’єктів від найменшого значення до найбільшого, а границі класів встановлюються в місцях порівняно великих стрибків значень;

– метод квантилів – кожному класу надається однакова кількість об’єктів з певного набору;

– рівноплощинний метод – дозволяє класифікувати тільки полігони за інтервалами в значеннях атрибутів (що мають дійсні значення) так, щоб загальна площа полігонів у кожному класі складала приблизно одну й ту ж величину;

– метод рівних інтервалів – значення атрибутів поділяються на рівні за розмірами підгрупи (підкласи);

– метод стандартних відхилень – показують різницю значення атрибута порівняно із середнім значенням усіх величин, тобто знаходиться середнє значення і потім розставляються інтервали вгору і вниз щодо середнього значення з визначеним кроком, поки всі значення даних не будуть занесені до свого класу.

Технологія класифікації об’єктів у ГІС передбачає перекодування атрибутів у таблицях або значень комірок растра для створення нових шарів. Найбільш простий випадок класифікації – перейменування полігонів на основі значень їхніх власних атрибутів. Більш складні випадки класифікації потребують розчинення меж угрупувань полігонів одного класу або визначення нового класу шляхом інтеграції властивостей багатьох шарів інформації. Досить часто підставою для визначення класів стає аналіз поверхонь.

Метод природних інтервалів утворює групи таким чином, що в середину класу потрапляють близькі між собою значення, а між класами існує істотна різниця. Межі класів визначаються там, де є різкий перепад між групами значень.

У цьому випадку ГІС автоматично визначає максимальне й мінімальні значення для кожного класу; використовуючи математичну процедуру, яка аналізує різкі зміни в даних. Ця процедура вибирає інтервали, які найкраще групують близькі значення, і максимізує відмінності між класами.

Переваги методу. Даний підхід є найбільш ефективним при картуванні даних, що мають нерівномірний розподіл, тому що природний розподіл об’єднує розкидані по карті близькі значення в один клас.

Недоліки методу. Труднощі зіставлення класів на різних картах, оскільки інтервали розподілу характерні тільки для даної вибірки. Однак дану проблему можна розв'язати шляхом використання для різних карт єдиної легенди, складеної методом природного розподілу на найбільш характерній вибірці.

Крім того, використання даного методу не рекомендується у випадку рівномірного розподілу даних, коли різкі зміни в значеннях недостатньо розізнаються.

На рисунку 17.2 проілюстровано дію методу природного розподілу при аналізі кількості населення та їх доходів за кварталами міста.

Рис. 17.2. Гістограма розподілу і результуюча карта після виконаний природного розподілу

Класи основані на природному групуванні значень даних. На гістограмі розподіл класів виконано так, що райони, які мають близькі значення, містяться в одному класі. Результуюча карта (рис. 17.3) підкреслює розбіжності між районами з різною кількістю населення.

Метод квантилів.Квантилі мають рівну кількість об'єктів у кожному класі. ГІС впорядковує об'єкти за принципом зміни їхнього атрибута в інтервалі від максимального до мінімального значення й підсумовує їхню кількість.

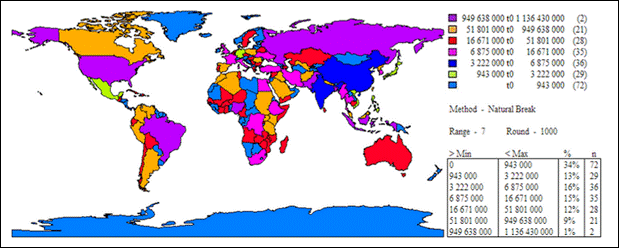
Рис. 17.3. Візуалізація карти чисельності населення країн світу методом природного розподілу

Потім ділить загальну кількість об'єктів на задане число класів, щоб отримати кількість об'єктів у кожному класі. Після цього присвоює першим по порядку об'єктам значення найнижчого класу, поки цей клас не буде заповнений, потім переміщається до наступного класу, заповнює його тощо.

Переваги методу:

– наочне зіставлення областей, розміри яких приблизно однакові;

– можливість ефективного відображення на карті об'єктів, значення яких розподілені рівномірно;

– можливість оцінити відносне положення об'єкта серед об'єктів оточення, наприклад, можна показати, які області в державі мають найбільший прибуток (входять до складу 20-відсоткової групи з найвищим значенням середнього прибутку) тощо.

Необхідно пам’ятати, що при розбивці на квантилі, об’єкти з близькими значеннями можуть потрапляти до різних класів, особливо, якщо значення розташовані щільно. Це може призвести до необґрунтованого їх розподілу, і навпаки – декілька далеко рознесених суміжних значень, можуть виявитися в одному класі, приховуючи відмінності між об’єктами.

Класифікація задопомогою квантилів може також змінювати реальні закономірності розподілу, якщо області мають істотну різницю в розмірах. Оскільки, як зазначалося, кожен клас містить рівну кількість об'єктів, на гістограмі заштриховано площі, що утворюють один клас і зазначено інтервали класу, де вони перетинають горизонтальну вісь. На карті (рис. 17.4) райони зподібними значеннями поміщено в суміжні класи, а райони з високими значеннями поєднані в один клас.

Рис. 17.4. Гістограма первісного розподілу об'єктів і результуюча карта після розподілу на квантилі

Метод рівних інтервалів.У даному випадку кожен клас має рівний діапазон значень, тому різниця між максимальним і мінімальним значенням однакова для кожного класу. ГІС віднімає мінімальне значення в наборі даних від максимального. Отримане значення ділиться на задану кількість класів. Граничне значення для першого класу отримується шляхом додавання результату ділення до найменшого значення вибірки. Якщо число записів не кратне кількості діапазонів, спірні записи призначаються у той діапазон, до якого ближче значення запису У такий спосіб встановлюються інтервали для іншої частини класів.

Метод дуже зручний для представлення інформації нетехнічній аудиторії. Рівні інтервали більш прості для розуміння, тому що діапазон для кожного класу однаковий. Ще краще, якщо одиниці вимірювання подані в відомих дослідникам (наприклад, відсотки).

Ефективність методу істотно знижується при оцінці нерівномірних розподілів, коли припускається можливість скупчення великої кількості об’єктів в одному чи двох класах при повній їхній відсутності в інших. На рис. 17.5 показано, як змінюється розподіл при рівномірній розбивці.

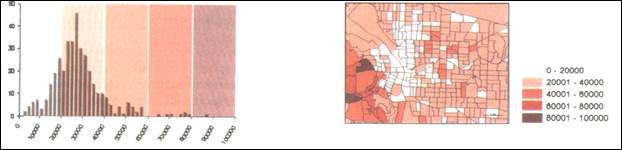
Рис. 17.5. Гістограма розподілу об'єктів і результуюча карта після розбивки на рівні інтервали

Різниця між максимальними й мінімальними значеннями у цьому випадку, однакова для кожного класу, тому на карті (рис. 17.6) майже всі райони містяться у трьох найнижчих класах. Таким чином, дана карта підкреслює наявність невеликої кількості районів з найбільшою кількістю населення.

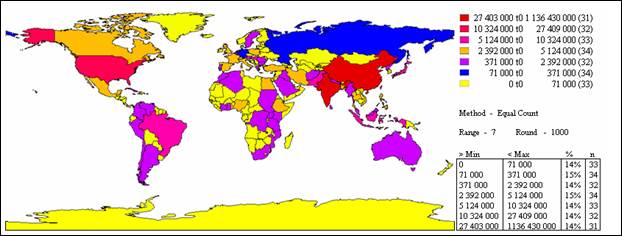
Рис. 17.6. Візуалізація карти чисельності населення країн світу методом рівних інтервалів

Метод стандартних відхилень.У даному випадку кожен клас визначається величиною відхилення від середнього у вибірці. ГІС спочатку знаходить середнє значення у вибірці, поділивши суму всіх значень на загальну кількість об'єктів. Після цього обчислюється середньоквадратичне відхилення шляхом віднімання середнього значення від кожного значення й піднесення отриманої різниці в квадрат (щоб забезпечити позитивне значення). Отримані значення підсумовуються й діляться на кількість об'єктів. З отриманого результату розраховується корінь. Формула виглядає таким чином:

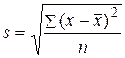
де s – середньоквадратичне відхилення;

х –значення об'єкта;

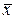– середнє за вибіркою;

п – кількість об'єктів.

Такий підхід дає можливість уявити напрямок відхилення параметра об'єкта від середнього значення у більший чи менший бік, а також зверну­ти увагу на дані, що мають у загальній масі невелике відхилення від середнього (логарифмічно нормальний чи нормальний розподіл). При цьому потрібно пам’ятати, що карта, отримана в результаті класифікації за середньоквадратичним відхиленням, ніколи не виявить реальні характеристики об'єкти. Її призначення - виявити тільки відхилення від середнього. Розглянемо ілюстрацію (рис. 17.7).

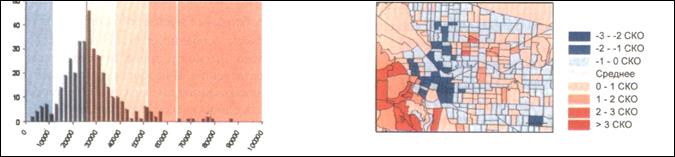
Рис. 17.7. Гістограма розподілу об'єктів і результуюча карта після розбивки за середньоквадратичним відхиленням

Об'єкти поділено на класи за значенням відхилення від середнього. ГІС обчислює середнє і стандартне відхилення. Потім послідовно додає середньоквадратичне відхилення до середнього чи віднімає його від середнього, щоб визначити інтервали класу. Карта (рис. 17.8) показує, наскільки відрізняються значення об'єктів від середнього.

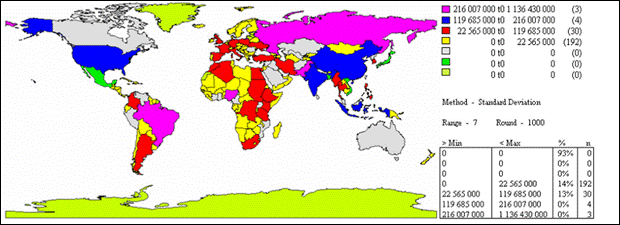
Рис. 17.8. Візуалізація карти чисельності населення країн світу методом середньоквадратичного відхилення