Обоснование и развитие единого расчетного аппарата для статистического контроля качества в дорожном строительстве
Контроль качества в дорожном строительстве имеет значительное отличие от контроля качества в других областях применения. Основные отличия связаны с линейностью объектов, разнообразием номенклатуры измеряемых параметров, значительной изменчивостью показателей во времени и по координатам, трудностью измерения большинства параметров.
В этой связи одной из актуальнейших проблем контроля качества в дорожном строительстве является разработка единого математического аппарата для контроля всего многообразия параметров, характеризующих качество автомобильной дороги. В настоящем разделе дается обоснование и развивается теоретический аппарат метода статистического контроля качества, применимого для контроля любого параметра дороги и ее конструктивных элементов.
В результате многолетних работ по контролю качества дорожного строительства в различных регионах России был сделан важный вывод, связанный с определением неоднородности контролируемых параметров, а также оценена неоднородность различных параметров дорожной одежды и земляного полотна. Результаты оценки показали, что неоднородность параметров в дорожном строительстве в несколько раз выше, чем в других отраслях. Так, неоднородность стали редко доходит до значений коэффициента вариации 0,05, в то же время для автомобильных дорог эти значения колеблются в пределах 0,01-2,2, то есть могут быть выше до 44 раз. Наибольшие значения коэффициентов вариации соответствуют механическим свойствам материалов, а также их геометрическим размерам. В значительно меньшей степени неоднородность присуща физическим свойствам материалов.
Ниже приведены опытные данные по коэффициентам вариации (табл. 36.1-36.3).
Таблица 36.1
Распределение коэффициентов вариации различных параметров
| Измеряемый параметр | Коэффициенты вариации | ||||||||
| 0,0-0,1 | 0,1-0,2 | 0,2-0,3 | 0,3-0,4 | 0,4-0,5 | 0,5-0,6 | 0,6-0,7 | 0,7-0,8 | 0,8-0,9 | |
| Частота появления различных значений коэффициентов вариации, % | |||||||||
| Упругая деформация асфальто- бетонной дорожной одежды | 1,8 | 17,8 | 33,9 | 28,6 | 12,5 | 1,8 | 1,8 | 1,8 | - |
| Толщина асфальтобетонного слоя | 2,7 | 46,0 | 29,7 | 13,5 | 5,4 | 2,7 | - | - | - |
| Упругая деформация слоя щебня, обработанного битумом | 14,3 | 14,3 | 14,3 | 28,6 | 28,5 | - | - | - | |
| Ровность слоя щебня, обработанного битумом | - | - | - | 11,1 | 11,1 | 22,2 | 55,6 | - | - |
| Толщина слоя щебня, обработанного битумом | 20,0 | 20,0 | 60,0 | - | - | - | - | - | - |
| Упругая деформация слоя щебня | - | - | 28,6 | 21,4 | 28,6 | 14,3 | - | - | 7,1 |
| Толщина слоя щебня | - | 33,3 | 11,1 | 44,4 | 11,2 | - | - | - | - |
| Упругая деформация слоя песка | - | - | 66,7 | 33,3 | - | - | - | - | - |
| Толщина слоя песка | - | 12,5 | 25,0 | 25,0 | 12,5 | 12,5 | 12,5 | - | - |
| Упругая деформация грунта | - | 6,2 | 18,8 | 18,8 | 24,9 | 12,5 | 18,8 | - | - |
| Температура асфальтобетонной смеси | 30,0 | 60,0 | 8,3 | 1,7 | - | - | - | - | - |
| Толщина слоя песчано-гравийной смеси | 10,3 | 48,3 | 27,6 | 13,8 | - | - | - | - | - |
Таблица 36.2
Распределение коэффициентов вариации плотности и ширины слоев
| Измеряемый параметр | Коэффициенты вариации | ||||||
| 0,01-0,02 | 0,02-0,03 | 0,03-0,04 | 0,04-0,05 | 0,05-0,06 | 0,06-0,07 | 0,08-0,09 | |
| Частота появления различных значений коэффициентов вариации, % | |||||||
| Ширина полосы асфальтобетона | 11,1 | 55,6 | 11,1 | 11,1 | 11,1 | - | - |
| Ширина проезжей части | 35,3 | 41,1 | 5,9 | 5,9 | 5,9 | 5,9 | |
| Плотность асфальтобетона | 5,8 | 6,7 | 8,3 | 16,7 | 24,9 | 29,2 | 8,4 |
Таблица 36.3
Распределение коэффициентов вариации ровности
| Измеряемый параметр | Коэффициенты вариации | |||||
| 0,4-0,6 | 0,6-0,8 | 0,8-1,0 | 1,0-1,2 | 1,2-1,4 | 1,4-2,0 | |
| Частота появления различных значений коэффициентов вариации, % | ||||||
| Ровность слоя асфальтобетона | 8,9 | 28,9 | 35,6 | 13,3 | 8,9 | 4,4 |
| Ровность поверхности земляного полотна | 12,5 | 37,5 | 37,5 | 12,5 | - | - |
Обработка экспериментальных данных по контролю качества конструктивных слоев дорожной одежды дала следующие значения коэффициентов вариации различных параметров (табл. 36.4).
Из табл. 36.1-36.4 видно, что коэффициенты вариации различных параметров колеблются в широких пределах от 0,0 до 2,0. Даже для одного параметра колебания коэффициентов вариации доходят до 5-10 раз. Следовательно, неучет однородности параметров может привести к принципиальным ошибкам в оценке качества строительства.
Таблица 36.4
Сводные данные по однородности измеряемых параметров
| Наименование слоя и контролируемые параметры | Значения коэффициентов вариации | ||
| минимальные | средние | максимальные | |
| Верхний слой асфальтобетона | |||
| прогибы | 0,173 | 0,383 | 0,030 |
| ровность | 0,535 | 0,844 | 1,671 |
| толщина | 0,171 | 0,276 | 0,649 |
| ширина | 0,020 | 0,029 | 0,049 |
| температура укладки | 0,540 | 0,083 | 0,095 |
| Нижний слой асфальтобетона | |||
| прогибы | 0,216 | 0,314 | 0,511 |
| ровность | 0,537 | 0,767 | 0,971 |
| толщина | 0,174 | 0,241 | 0,317 |
| ширина | 0,010 | 0,035 | 0,055 |
| Щебень | |||
| прогибы | 0,296 | 0,512 | 0,942 |
| ровность | 0,426 | 0,595 | 0,704 |
| толщина | 0,105 | 0,233 | 0,463 |
| Песок | |||
| прогибы | 0,237 | 0,395 | 0,488 |
| толщина | 0,314 | 0,345 | 0,400 |
| Грунтовое основание | |||
| прогибы | 0,230 | 0,463 | 0,688 |
| ровность | 0,760 | 0,844 | 0,914 |
По результатам контроля качества получены осредненные значения коэффициентов вариации различных параметров, необходимые для расчета требуемого количества измерений.
Принципиальное значение для обоснования математического аппарата контроля качества имеет закон распределения случайной величины (значений толщины, ширины, ровности и т.п.). Все классические методы контроля качества базируются на законе нормального распределения, то есть симметричного закона. Однако даже беглый анализ данных контроля (см. табл. 36.1-36.3) говорит о том, что распределение многих параметров дороги не может подчиняться этому закону.
В частности, исследования показали, что для упругих деформаций дорожных одежд при значительных коэффициентах вариации (более 0,33) лучшие результаты дает закон Вейбулла. При меньших значениях коэффициентов вариации несколько лучшие результаты дает нормальный закон, хотя закон Вейбулла в 38 случаях из 100 также дает лучшие результаты.
Аналогичное сопоставление было проведено и для других параметров дорожной одежды и земляного полотна. Результаты обработки экспериментальных данных (рис. 36.1) показывают, что распределение толщин слоев, ровности, упругих деформаций во многих случаях несимметричное, поэтому не может быть описано нормальным законом распределения.
Было предложено использовать в контроле качества дорожного строительства закон распределения Вейбулла с переменными параметрами. Математическая запись этого закона при двух параметрах имеет вид
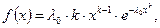 где (36.3)
где (36.3)
f(x) - плотность распределения случайной величины X;
λ0 - параметр масштаба;
k - параметр формы.
Для определения параметров распределения можно использовать формулы
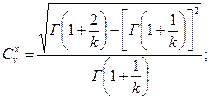 (36.4)
(36.4)
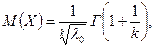 где (36.5)
где (36.5)
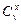 и М(Х) - коэффициент вариации и математическое ожидание (среднее значение) измеряемой величины;
и М(Х) - коэффициент вариации и математическое ожидание (среднее значение) измеряемой величины;
Г - гамма-функция.
По найденным при измерении значениям 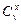 и М(Х) нетрудно рассчитать величины параметров k, λ0.
и М(Х) нетрудно рассчитать величины параметров k, λ0.
Анализ формул (36.3-36.5) показал, что законом Вейбулла с переменными параметрами можно описать любые экспериментальные данные, так как при К = 1 этот закон превращается в экспоненциальный, которым можно аппроксимировать данные контроля, например, ровности, при К ³ 4 он превращается в нормальный закон, что позволяет использовать его для описания законов распределения плотности, толщин слоев, упругих деформаций, ширины и т.п.
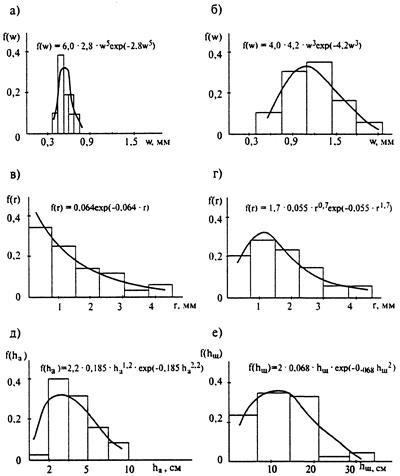
Рис. 36.1. Аппроксимация экспериментальных данных теоретическими законами распределения случайных величин:
А - упругие деформации при высокой однородности; б - то же при низкой однородности; в - ровность при значении коэффициента вариации 1; г - то же при значении коэффициента вариации 0,8; д - толщина слоя асфальтобетона; е - толщина слоя щебня
Следовательно, появилась возможность разработать единый расчетный аппарат для любых параметров дороги.
Экстремальные (крайние) значения контролируемых параметров могут быть рассчитаны по следующим формулам
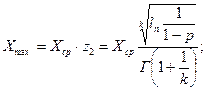 (36.6)
(36.6)
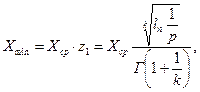 где (36.7)
где (36.7)
Р - доверительная вероятность;
k - коэффициент формы;
z1, z2 - коэффициент перехода от среднего к экстремальным значениям;
Хcр - среднее значение параметра.
По полученным формулам построена расчетная номограмма (рис. 36.2), по которой можно определить экстремальные значения контролируемой величины при определенной доверительной вероятности.
Для определения количества выходов измеряемой величины за какой-либо допуск находится показатель дефектности - Д
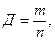 где (36.8)
где (36.8)
m - число измерений, выходящих за пределы допуска;
n - общее число измерений при контроле.
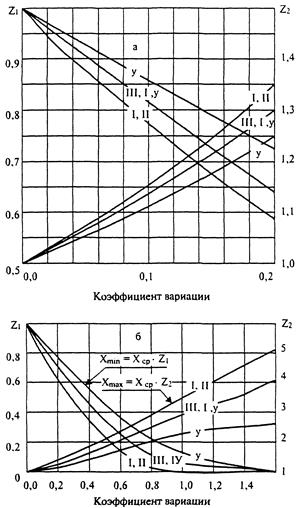
Рис 36.2. Номограмма для определения значений z1 и z2 (римскими цифрами на кривых обозначены категории дорог):
а - для малых значений Cv; б - для больших значений Cv.
Чтобы определить показатель дефектности для закона Вейбулла с переменными параметрами можно воспользоваться схемой, изображенной на рис. 36.3.
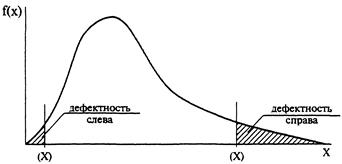
Рис. 36.3.. Схема определения показателя дефектности для закона Вейбулла
При ограничении величины справа (по максимальному значению) показатель дефектности находится следующим образом
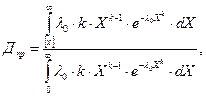 (36.9)
(36.9)
Используя формулу (36.5), преобразуем выражение (36.9)
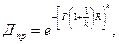 где (36.10)
где (36.10)
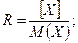 (36.11)
(36.11)
[X] - допустимое значение контролируемого параметра, определяемое по нормативным документам;
М(Х) - математическое ожидание контролируемого параметра.
Аналогично находится дефектность при ограничении слева (по минимальному значению).
По полученным формулам построена расчетная номограмма (рис. 36.4), с помощью которой можно определить дефектность контролируемого параметра.
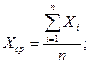 (36.12)
(36.12)
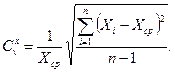 (36.13)
(36.13)
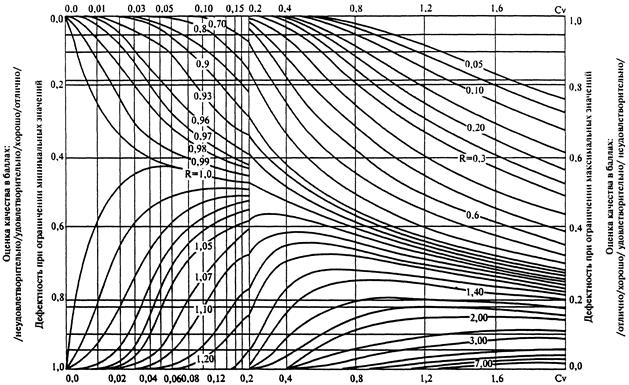
Рис. 36.4. Номограмма для определения значения показателя дефектности и оценки качества для контролируемого параметра
Имеется много разных способов упрощенного подсчета статистических характеристик. Достаточной точностью обладает способ их определения по медиане и размаху. С этой целью измеренные величины выстраиваются в ранжированный ряд по возрастающим значениям. Крайние члены проверяют на принадлежность ряду. Для этого находят критерии τ для минимальных и максимальных значений параметра в ряду и сравнивают их с табличными значениями критерия τкр (табл. 36.5).
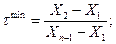
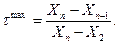 (36.14)
(36.14)
Если значение τ больше τкрит , то крайний член ряда отбрасывают и получают улучшенный ряд. При необходимости проверяют крайние члены полученного улучшенного ряда до тех пор, пока фактические значения критерия τ не станут меньше τкрит.
Для еще большего упрощения улучшение ряда производят простым отбрасыванием минимального и максимального значений ряда. В этом случае имеется, хотя и небольшая, вероятность сохранения в ряду «сомнительного» значения измеряемого параметра.
По упрощенной методике математическое ожидание измеряемой величины находится как медиана улучшенного ряда. Так, если в ряду осталось 13 членов, то медианным значением будет седьмой член ряда. Если число членов ряда четное (например 14), то медиана находится как полусумма 7 и 8 членов ряда.
Таблица 36.5
Критические значения критерия τ
| Число членов ряда | τкрит | Число членов ряда | τкрит | Число членов ряда | τкрит |
| 0,9555 | 0,45 | 0,309 | |||
| 0,807 | 0,428 | 0,299 | |||
| 0,689 | 0,395 | 0,291 | |||
| 0,61 | 0,369 | 0,283 | |||
| 0,554 | 0,349 | 0,279 | |||
| 0,512 | 0,334 | 0,276 | |||
| 0,477 | 0,320 | 0,274 |
Коэффициент вариации по упрощенной методике находится как:
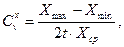 где (36.15)
где (36.15)
t - коэффициент нормированного отклонения (табл. 36.6), принимаемый в зависимости от доверительной вероятности или категории дороги, числа испытаний и вида ограничений.
Приведенная формула действительна для параметров с малыми значениями коэффициентов вариации - до 0,2 (таких как плотность, ширина, толщина слоев и т.п.). Для параметров с коэффициентами вариации более 0,2 (таких как ровность, водонасыщение, модуль упругости и т.п.) значение 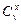 целесообразно определять по рис. 36.2. С этой целью находится величина коэффициента z2 по формуле
целесообразно определять по рис. 36.2. С этой целью находится величина коэффициента z2 по формуле
z2 = Xmax/Xср, (36.16)
а затем по рис. 36.2 для соответствующей категории дороги находится коэффициент вариации. По номограмме на рис. 36.2 можно определять и малые значения коэффициентов вариации. При использовании данных из табл. 36.6 следует иметь в виду, что одностороннее ограничение накладывается на измерение плотности упругих деформаций, ровности и др., двустороннее ограничение - на толщину и ширину слоев и др.
При составлении табл. 36.6 приняты следующие значения доверительной вероятности, установленные в результате обобщения опубликованных данных: для дорог I-II технических категорий - 0,95, для III-IV - 0,90, для V - 0,85.
Данный метод учитывает специфику дорожного строительства и является общим для измерения любых параметров дороги.
Таблица 36.6
Значение нормируемого отклонения t
| Число членов улучшенного ряда | Значение t при одностороннем ограничении параметра для категорий дороги | |||
| - | I-II | III-IV | V | |
| 4,54 | 3,18 | 2,35 | 1,64 | |
| 3,36 | 2,57 | 2,01 | 1,48 | |
| 3,00 | 2,37 | 1,90 | 1,41 | |
| 2,82 | 2,26 | 1,83 | 1,38 | |
| 2,72 | 2,20 | 1,80 | 1,36 | |
| 2,65 | 2,16 | 1,77 | 1,35 | |
| 2,60 | 2,13 | 1,75 | 1,34 | |
| 2,57 | 2,11 | 1,74 | 1,33 | |
| 2,54 | 2,09 | 1,73 | 1,32 | |
| 2,49 | 2,06 | 1,71 | 1,32 | |
| 2,46 | 2,04 | 1,70 | 1,31 | |
| 2,42 | 2,02 | 1,68 | 1,30 | |
| 2,39 | 2,00 | 1,67 | 1,30 | |
| - | I-II | III-IV | V | - |
| Значение t при двустороннем ограничении параметра для категории дороги |
Дата добавления: 2021-09-07; просмотров: 549;











