Закон распределения. ЭксТракция.
Если мы имеем две несмешивающиеся жидкости и добавляем туда третий компонент, который растворяется в обеих жидкостях, то отношение концентраций этого компонента есть величина постоянная при данной температуре.
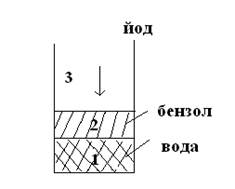
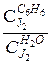 = К, где К – коэффициент распределения йода между водой и бензолом.
= К, где К – коэффициент распределения йода между водой и бензолом.
В общем виде K= 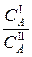 – закон распределения(1)
– закон распределения(1)
При постоянной температуре коэффициент распределения К есть величина постоянная, т.е. К не зависит:
1) от соотношения объемов жидкостей;
2) от количества добавленного йода.
В такой форме закон распределения справедлив только в том случае, если распределяемое вещество имеет одинаковую молярную массу в обоих растворителях.
Отклонение от закона распределения наблюдается в том случае, если распределяемое вещество ассоциирует или диссоциирует в одной из фаз.
К= 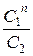 , (2)
, (2)
если n=1, то молекулярное состояние не меняется;
если n>1, то идет диссоциация;
если n<1, то идет ассоциация.
Чтобы найти, т.е. определить состояние растворенного вещества в одной из фаз, нужно линеизировать уравнение (2). Логарифмируем уравнение (2) и получаем:
ln K=n∙ln 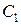 -ln
-ln 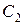 или
или
ln 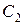 =n∙ln
=n∙ln 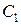 -ln K (*)
-ln K (*)
На основе уравнения (*) можно построить график:
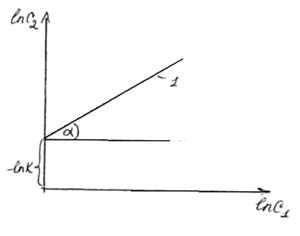
tg 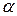 =n
=n
Прямая 1 характеризует зависимость ln 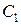 от ln
от ln 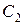 . Член уравнения – ln K определяет расстояние прямой 1 от оси Х. Тангенс угла наклона прямой дает значение n.
. Член уравнения – ln K определяет расстояние прямой 1 от оси Х. Тангенс угла наклона прямой дает значение n.
Экстракция– это извлечение одного вещества из многокомпонентной системы посредством третьего компонента, который называется экстрагентом.
Требования к экстрагенту:
1) Экстрагент не должен смешиваться с растворителем, из которого происходит экстрация.
2) Экстрагент должен избирательно растворять выделяемое вещество.
3) Наилучшая степень извлечения достигается при добавлении экстрагента небольшими порциями.
4) Количество вещества, извлеченного в результате экстракции, определяется следующими соотношениями:
К= 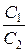 , где
, где
С 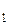 – концентрация вещества, оставшегося в системе после первой экстракции;
– концентрация вещества, оставшегося в системе после первой экстракции;
С 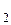 – количество вещества, удаляемого из системы в результате экстракции.
– количество вещества, удаляемого из системы в результате экстракции.
С 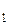 =
= 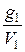 ;C
;C 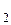 =
= 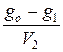 , где
, где
g 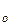 – масса экстрагируемого вещества до экстракции;
– масса экстрагируемого вещества до экстракции;
g 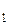 – масса вещества, оставшегося после экстракции;
– масса вещества, оставшегося после экстракции;
V 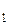 – объем растворителя, в котором добавляется экстрагент;
– объем растворителя, в котором добавляется экстрагент;
V 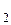 – объем экстрагента;
– объем экстрагента;
К – коэффициент распределения (из справочника).
Подставим эти выражения в уравнение коэффициента распределения и получим:
К= 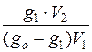
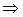
g 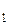 =g
=g 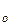
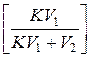 – для однократной экстракции
– для однократной экстракции
g 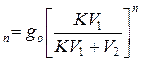 – для многократной экстракции
– для многократной экстракции
где n – количество добавляемых порций экстрагента; g 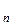 – масса оставшегося после экстракции вещества.
– масса оставшегося после экстракции вещества.
g 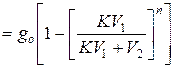
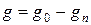 – количество экстрагируемого вещества.
– количество экстрагируемого вещества.
ПРИМЕР.
| Дано: | Решение: |
V  (H (H 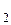 O)=2000 мл
g O)=2000 мл
g 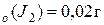 V
V  (CS (CS 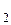 )=50 мл
К= )=50 мл
К= 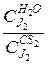 =0,00167
g =0,00167
g 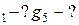
|
1) Однократная экстракция всем объемом растворителя – экстрагента:
g 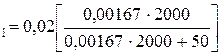 =0,00125 г
2) Проведем экстракцию 5 раз порциями экстрагента по 10 мл: =0,00125 г
2) Проведем экстракцию 5 раз порциями экстрагента по 10 мл:
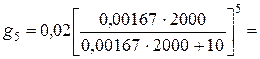 0,0000197 г
Второй метод более выгоден, т.к. йода в воде останется меньше. 0,0000197 г
Второй метод более выгоден, т.к. йода в воде останется меньше.
|
Дата добавления: 2017-09-01; просмотров: 2610;











