Теорема об изменении кинетического момента системы в относительном движении по отношению к центру масс

Пусть механическая система совершает движение относительно основной системы координат 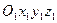. Возьмем подвижную систему координат 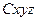с началом в центре масс системы 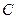, движущуюся поступательно относительно основной системы координат. Можно доказать справедливость формулы:

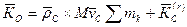, (177)

где 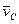– абсолютная скорость центра масс, .

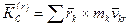Величина 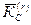является кинетическим моментом системы относительно центра масс для относительного движения относительно системы координат, движущейся поступательно вместе с центром масс, т. е. системы .

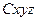Формула (176) показывает, что кинетический момент абсолютного движения системы относительно неподвижной точки 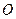равен векторной сумме кинетического момента центра масс относительно той же точки, если бы в центре масс была сосредоточена вся масса системы, и кинетического момента системы относительно центра масс для относительного движение системы по отношению к подвижной системе координат, движущейся поступательно вместе с центром масс.

Теорема об изменении кинетического момента системы относительно центра масс для относительного движения системы по отношению к системе координат, движущейся поступательно с центром масс; она формулируется так же, как если бы центр масс был неподвижной точкой:

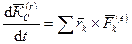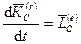или , (178)

где 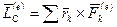является главным моментом всех внешних сил относительно центра масс.