Вращение твердого тела вокруг неподвижной оси
Вращением твердого тела вокруг неподвижной оси (оси вращения) называется такое его движение, при котором точки тела, лежащие на оси вращения, остаются неподвижными в течение всего времени движения.
Пусть осью вращения является ось 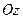 , которая может иметь в пространстве любое направление. Одно направление оси
, которая может иметь в пространстве любое направление. Одно направление оси 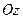 принимается за положительное (рис. 28).
принимается за положительное (рис. 28).

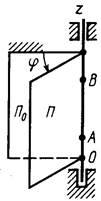 Через ось вращения проведем неподвижную плоскость
Через ось вращения проведем неподвижную плоскость 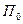 и подвижную
и подвижную 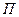 , скрепленную с вращающимся телом. Пусть в начальный момент времени обе плоскости совпадают. Тогда в момент времени
, скрепленную с вращающимся телом. Пусть в начальный момент времени обе плоскости совпадают. Тогда в момент времени 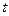 положение подвижной плоскости и самого вращающегося тела можно определить двугранным углом между плоскостями и соответствующим линейным углом
положение подвижной плоскости и самого вращающегося тела можно определить двугранным углом между плоскостями и соответствующим линейным углом 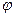 между прямыми, расположенными в этих плоскостях и перпендикулярными оси вращения. Угол
между прямыми, расположенными в этих плоскостях и перпендикулярными оси вращения. Угол 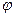 называется углом поворота тела.
называется углом поворота тела.
Положение тела относительно выбранной системы отсчета полностью определяется в любой момент времени, если задано уравнение
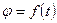 , (67)
, (67)
где 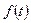 – любая, дважды дифференцируемая функция времени. Это уравнение называют уравнением вращения твердого тела вокруг неподвижной оси.
– любая, дважды дифференцируемая функция времени. Это уравнение называют уравнением вращения твердого тела вокруг неподвижной оси.
У тела, совершающего вращение вокруг неподвижной оси, одна степень свободы, так как его положение определяется заданием только одного параметра – угла 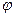 .
.
Угол 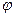 считается положительным, если он откладывается против часовой стрелки, и отрицательным – в противоположном направлении, если смотреть с положительного направления оси
считается положительным, если он откладывается против часовой стрелки, и отрицательным – в противоположном направлении, если смотреть с положительного направления оси 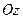 . Траектории точек тела при его вращении вокруг неподвижной оси являются окружностями, расположенными в плоскостях, перпендикулярных оси вращения.
. Траектории точек тела при его вращении вокруг неподвижной оси являются окружностями, расположенными в плоскостях, перпендикулярных оси вращения.
Для характеристики вращательного движения твердого тела вокруг неподвижной оси введем понятия угловой скорости и углового ускорения. Алгебраической угловой скоростью тела в какой-либо момент времени называют первую производную по времени от угла поворота в этот момент, т.е. 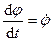 . Она является величиной положительной при вращении тела против часовой стрелки, так как угол поворота возрастает с течением времени, и отрицательной – при вращении тела по часовой стрелке, потому что угол поворота при этом убывает.
. Она является величиной положительной при вращении тела против часовой стрелки, так как угол поворота возрастает с течением времени, и отрицательной – при вращении тела по часовой стрелке, потому что угол поворота при этом убывает.
Модуль угловой скорости обозначают 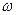 . Тогда
. Тогда
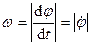 . (68)
. (68)
Алгебраическим угловым ускорением тела называют первую производную по времени от алгебраической скорости, т.е. вторую производную от угла поворота 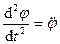 . Модуль углового ускорения обозначим
. Модуль углового ускорения обозначим 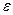 , тогда
, тогда
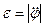 . (69)
. (69)
Если 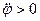 при
при 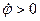 , то алгебраическая угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону (против часовой стрелки). При
, то алгебраическая угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону (против часовой стрелки). При 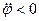 и
и 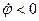 , тело вращается ускоренно в отрицательную сторону. Если
, тело вращается ускоренно в отрицательную сторону. Если 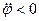 при
при 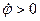 , то имеем замедленное вращение в положительную сторону. При
, то имеем замедленное вращение в положительную сторону. При 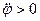 и
и 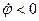 замедленное вращение совершается в отрицательную сторону.
замедленное вращение совершается в отрицательную сторону.
Угловую скорость и угловое ускорение на рисунках изображают дуговыми стрелками вокруг оси вращения. Дуговая стрелка для угловой скорости указывает направление вращения тела. Для ускоренного вращения дуговые стрелки для угловой скорости и углового ускорения имеют одинаковые направления, для замедленного – их направления противоположны.
Дата добавления: 2017-09-01; просмотров: 1604;











