Напряжение. Тензор напряжений
Многие механические свойства выражаются через величинунапряжений. В механике напряжения обычно рассматриваются как удельные характеристики сил, возникающих в теле под действием внешних нагрузок.
В простейшем случае осевого растяжения стержня определяются как
S=P/F,
где S - напряжение в сечении площадью F, перпендикулярном оси образца, вдоль которой действует сила P.
Размерность МПа или кгс/мм2 (1 кгс/мм2 =9,8 МПа).
В общем случае сила не перпендикулярна плоскости площадки, на которую она действует. Тогда ее, как любой вектор, можно разложить на две составляющие: нормальную (перпендикулярную к площадке), создающую нормальное напряжение, и касательную, действующую в плоскости площадки и вызывающую касательное напряжение. В механических испытаниях определяют именно эти напряжения. Их же используют в расчетах на прочность. Т.о., процессы при деформации и разрушении определяются касательными напряжениями (пластическая деформация, разрушение путем среза) и нормальными (разрушение отрывом) (рис. 17).
Нормальное напряжение в сечении Fa
S=(P/F0 )cos2 a,
а касательное
t= (P/F0 )cos a sin a = ½ (P/F0) sin 2a.
Максимальные нормальные растяжения возникают при a =0 , т.е. в площадках, перпендикулярных оси растяжения, а касательные напряжения достигают наибольших значений при a=450.
Нормальные напряжения делят на растягивающие (положительные) и сжимающие (отрицательные).
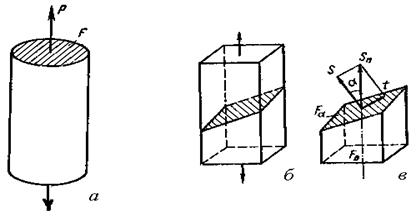
Рис. 17. Схема определения напряжения (а) и схемы определения составляющих полного напряжения (б и в).
Если не учитываются изменения величины площадки в процессе деформации, а напряжение рассчитывают как отношение нагрузки к исходной площадке сечения, то действующие напряжения называют условными. Если относят силу к величине фактического сечения, то такое напряжение называют истинным. В дальнейшем истинные напряжения будем обозначать символами S (нормальные) и t (касательные), а условные - s и t соответственно. При решении реальных задач необходимо иметь возможность оценить напряжения, действующие в любом сечении тела. Для этого используют представления о тензоре напряжений.
Внутри тела, находящегося под действием напряжений, всегда можно выделить бесконечно малый параллелепипед, ребра которого параллельны произвольно выбранным осям координат. В общем случае на три его непараллельные грани действуют взаимно уравновешенные векторы напряжений, которые можно разложить на нормальные и касательные составляющие. В результате параллелепипед находится под действием девяти напряжений: трех нормальных (Sx ,Sy , Sz) и шести касательных (txy ,t xz , t yz , tzy , t zx ,t yx) (рис. 18). Совокупность этих напряжений и есть тензор напряжений, который записывается как

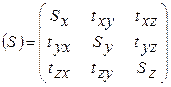
Чтобы выбранный параллелепипед находился в равновесии, необходимо равенство моментов относительно координатных осей. Поэтому по закону парности касательных напряжений тензор содержит фактически не девять, а шесть независимых напряжений. С помощью их можно охарактеризовать любое сложное напряженное состояние. Тензор позволяет определить величину нормальных и касательных напряжений в любой площадке, проходящей через данную точку тела, если известны ее направляющие косинусы (косинус угла между нормалью к площадке и соответствующей осью координат) относительно выбранных координатных осей.
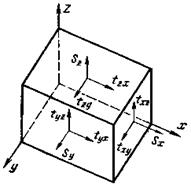
Рис.18. Взаимно уравновешенные напряжения, действующие на грани параллелепипеда.
В теории упругости доказывается, что при любом напряженном состоянии через каждую точку тела можно провести, по меньшей мере, три взаимно перпендикулярные площадки, на которых касательные напряжения нулевые и, следовательно, действуют только нормальные напряжения. Такие площадки и направления нормалей к ним называются главными площадками и главными направлениями напряжений, а действующие на этих площадках напряжения – главными нормальными напряжениями. При механических испытаниях главные направления напряжений обычно заранее известны, и их можно выбрать в качестве координатных осей. Тогда тензор напряжений упрощается до вида
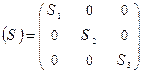
При таком упрощенном тензоре напряжений нормальные и касательные напряжения в заданной площадке с направляющими косинусами аx, ay, az рассчитывают как
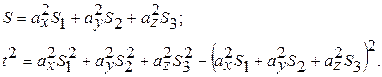
Как уже отмечалось, максимальные касательные напряжения действуют на площадках, расположенных под углом 450 к главным осям. Их величина равна полуразности соответствующих главных нормальных напряжений
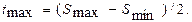
Главные касательные напряжения, действующие на трех взаимно перпендикулярных площадках, расположенных под углом 450 к главным осям, рассчитывают по формулам
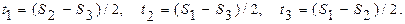
Дата добавления: 2017-09-01; просмотров: 2629;











