Дифференциальное уравнение и система дифференциальных уравнений для функций перемещений и усилий.

При выводе трехчленной формулы для нормальных напряжений было получено соотношение 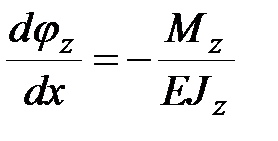(см. (9.14)), связывающие изгибающий момент 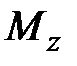и создаваемый им угол искривления элемента стержня 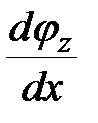(взаимный угол поворота торцов элемента 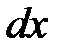– кривизна оси элемента).

Опуская индексz в обозначениях с учетом (13.1) получим систему двух дифференциальных уравнений первого порядка

, .

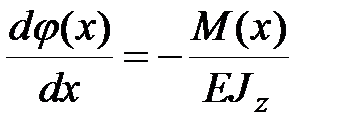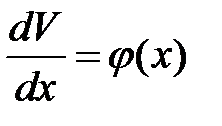(13.2)

Интегрирование системы уравнений (13.2) с учетом условий закрепления балки дает возможность найти функции 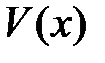и .

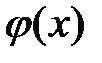Подстановка 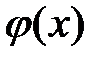из второго уравнения системы (13.2) в первое дает дифференциальное уравнение второго порядка относительно функции прогиба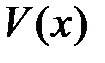

.

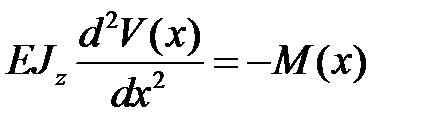(13.3)

С учетом известных дифференциальных соотношений между поперечной силой и интенсивностью распределенной нагрузки (7.3) 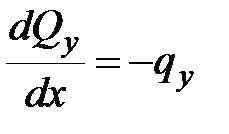, между изгибающим моментом и поперечной силой (7.4) 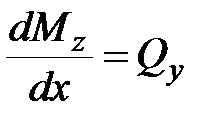, а также (13.2) получим:

, , , .

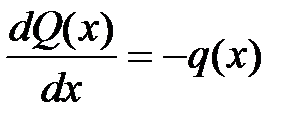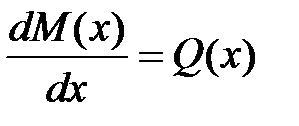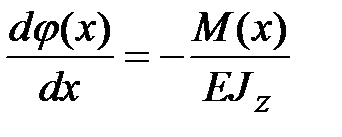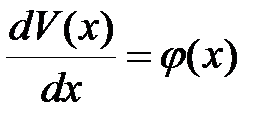(13.4)

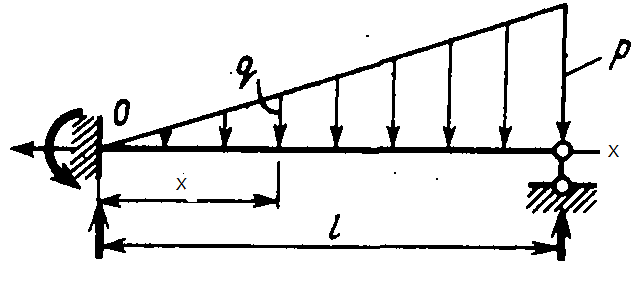
Интегрирование системы четырех обыкновенных дифференциальных уравнений первого порядка (13.4) выполняется с учетом граничных условий:

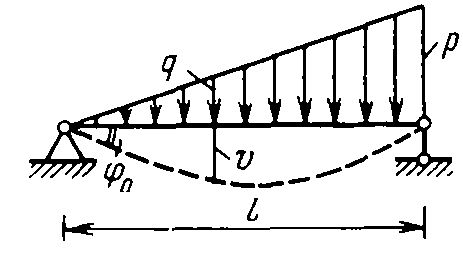
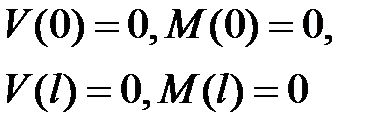
		(13.5)
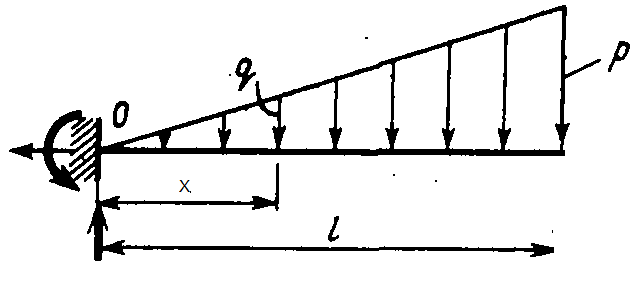
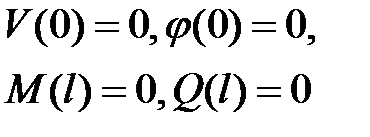
		(13.6)
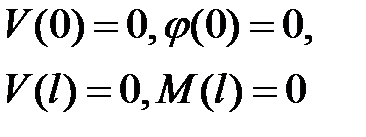
		(13.7)