Использование локальной системы координат при наличии нескольких участков интегрирования.

Пример 13.3

a = 3.9м, b = 0.9м, c = 1.2м, 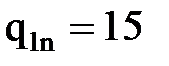кН/м , 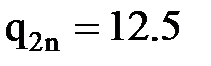кН/м ,

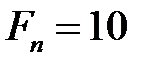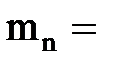кН, 5кН×м, ;

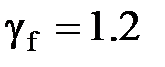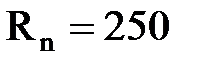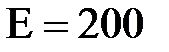сталь: МПа, ГПа, ;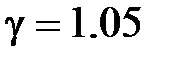

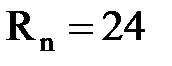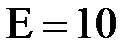древесина: МПа, ГПа, .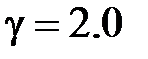

Расчетные нагрузки:

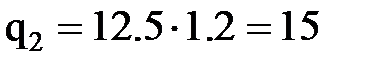кН/м, кН/м, 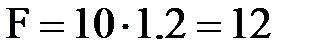кН ,

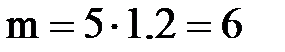кН×м.

Расчетная схема балки приведена на рис. 13.5

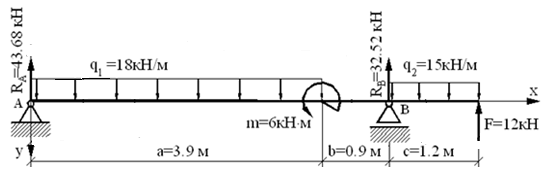
Рис.13.5 Расчетная схема балки

Выражения для изгибающих моментов на участках имеют вид (см. лекцию №12 пример 12.1):

, , .

( )

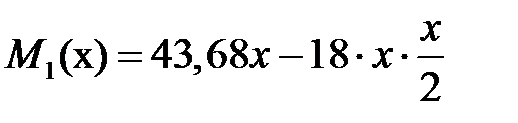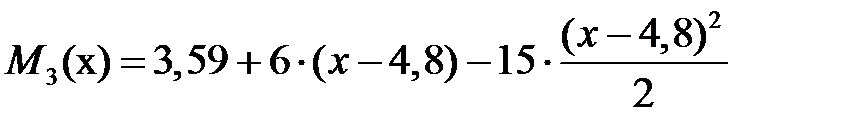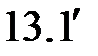Записываем дифференциальное уравнение оси изогнутой балки на первом участке и дважды его интегрируем

Первый участок , ,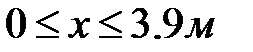

( )   ( )   ( )

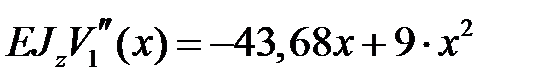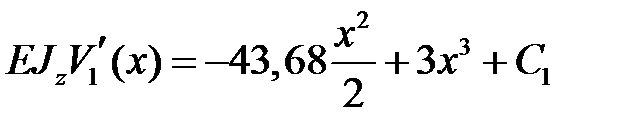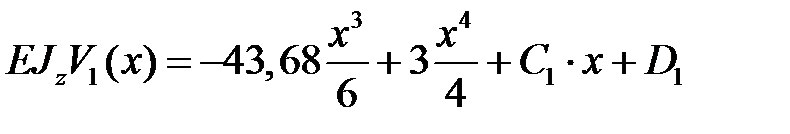
Записываем дифференциальное уравнение оси изогнутой балки на втором участке и дважды его интегрируем

Второй участок , , .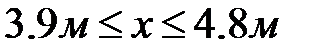

( )     ( )   ( )

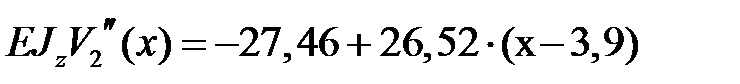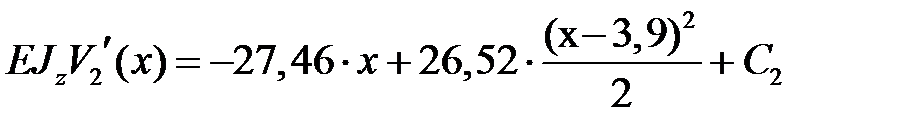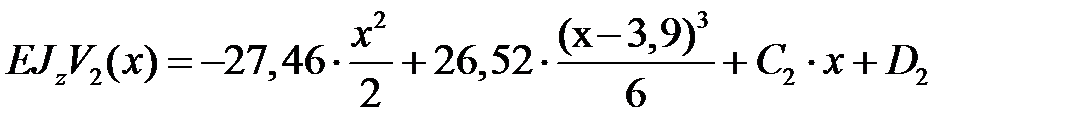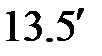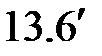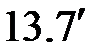Записываем дифференциальное уравнение оси изогнутой балки на третьем участке и дважды его интегрируем

Третий участок , , .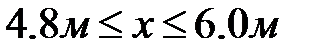

( )     ( )   ( )

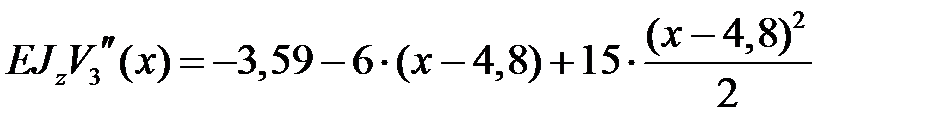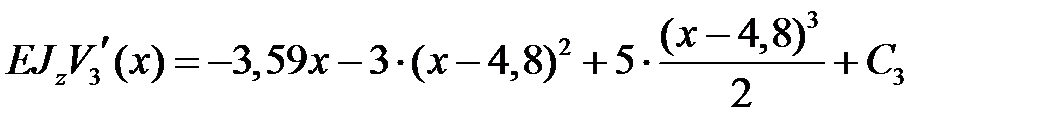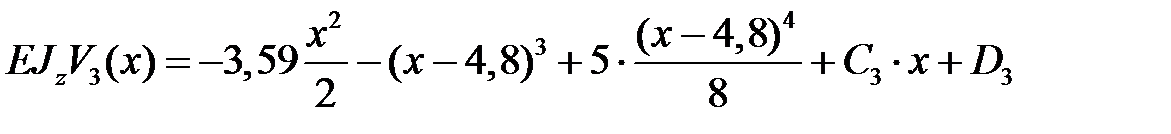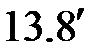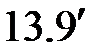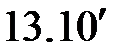Константы интегрирования определим из условий закрепления балки и условий непрерывности функции прогиба и ее производной на границах участков.

На левом конце балка опирается на опору, прогиб в точке равен нулю 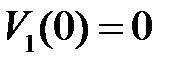, следовательно

.

( )

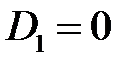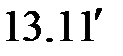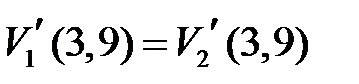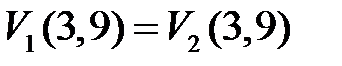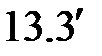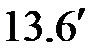Условия сопряжения на границе 1-го и 2-го участков имеют вид: , . С учетом выражений ( ) и ( ) получим

.

( )

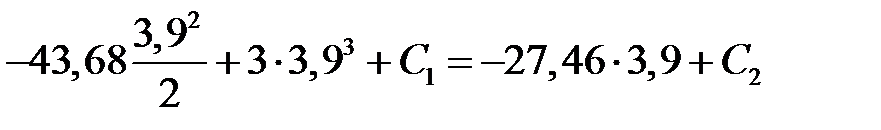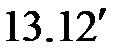С учетом выражени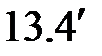й ( ) и ( 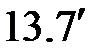) будем иметь

.

( )

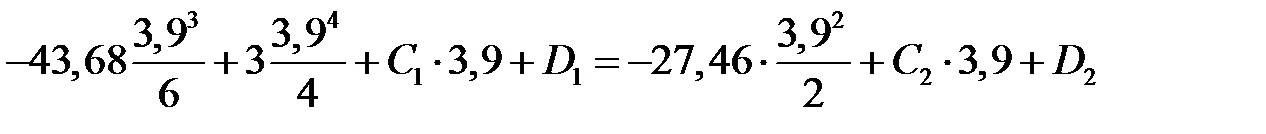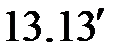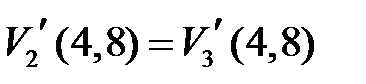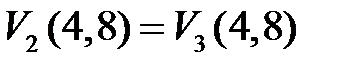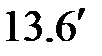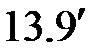Условия сопряжения на границе 2-го и 3-го участков имеют вид: , . С учетом выражений ( ) и ( ) получим

( )

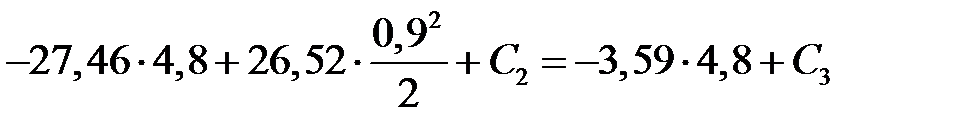
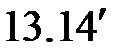С учетом выражени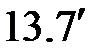й ( ) и ( 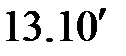) будем иметь

.

( )

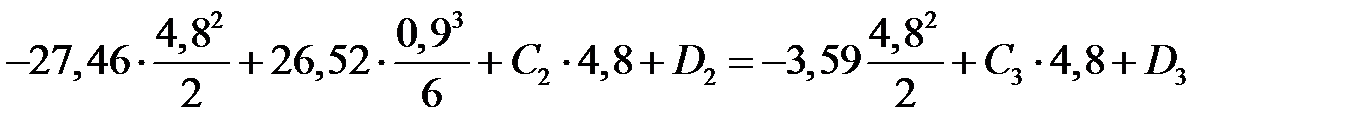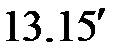В точке 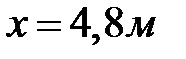балка опирается на опору, прогиб в точке равен нулю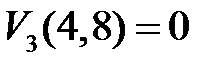

( )

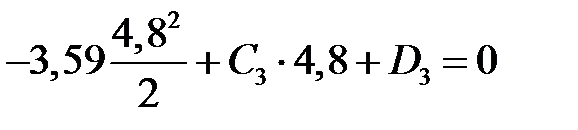
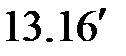Уравнения ( 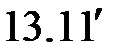)-( ) 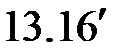образуют систему линейных алгебраических уравнений, которая имеет вид:

, , , ,

( )

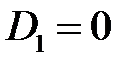
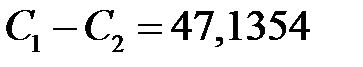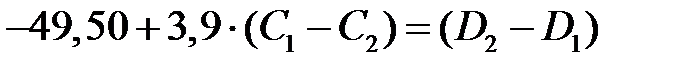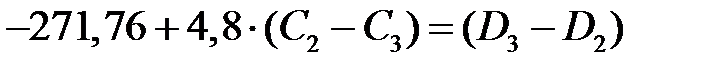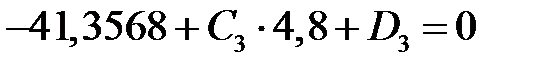
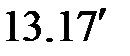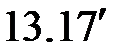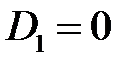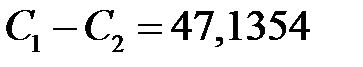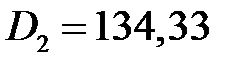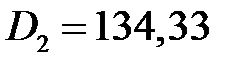Система уравнений ( ) легко разрешима. Действительно, из 1-го и 2-го уравнений имеем: , , тогда из 3-го уравнения находим . Используем 4-е уравнение , тогда с учетом из 5-го получаем 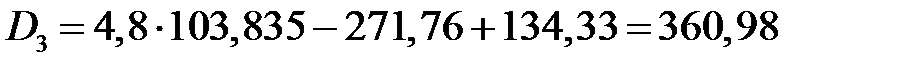. Подставляем 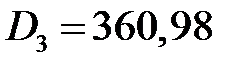в 6-е уравнение, находим 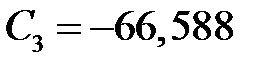. Из 4-го определяем 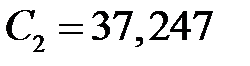. Из 2-го уравнения находим .

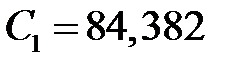Результат решения системы: ; ; ; ; ; .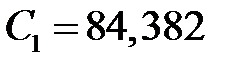

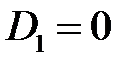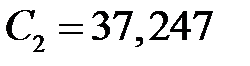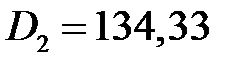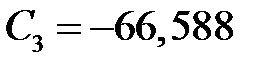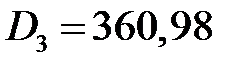Подставляем значения констант интегрирования в выражения для прогибов и углов поворота, получаем:

,

,

,

,

,

.

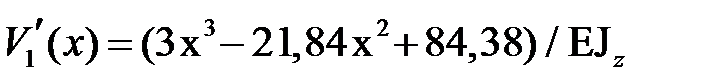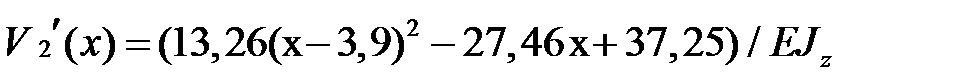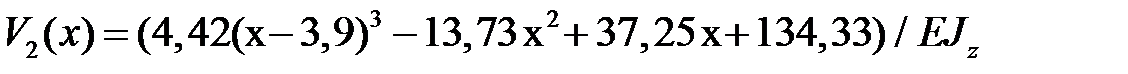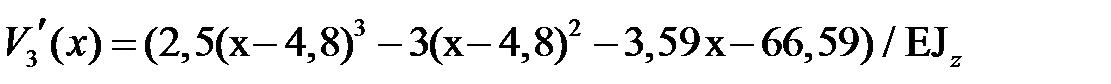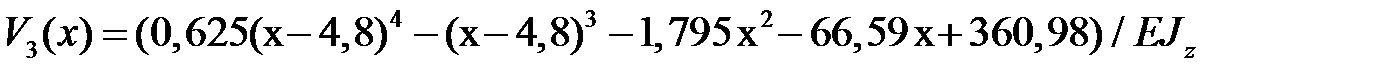При решении задачи использованы выражения для изгибающих моментов, полученные от действия расчетной нагрузки. Прогибы и углы поворота сечений балки определяются от действия нормативной нагрузки. Поэтому при вычислении перемещений их численные значения необходимо разделить на коэффициент надежности по нагрузке .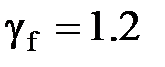

Прогиб в середине пролета балки от нормативной нагрузки

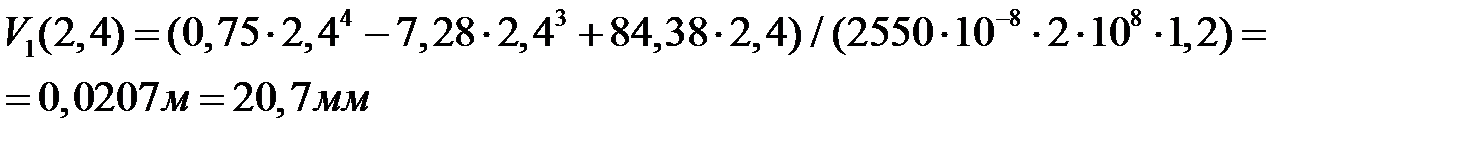
Прогиб на конце консоли от нормативной нагрузки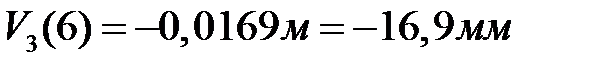

Угол поворота сечения на левой опоре от нормативной нагрузки 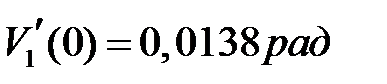. Угол поворота сечения на правой опоре .

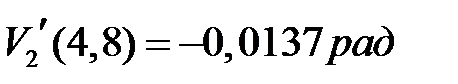Эпюры углов поворота сечений и прогибов представлены на рис. 13.6, 13.7.

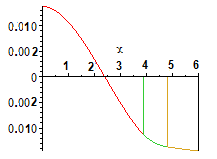Рис. 13. 6 Углы поворота сечений

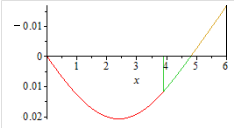Рис. 13.7 Прогибы

Точка, в которой 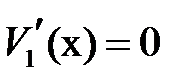, определяется из решения кубического уравнения

.

Корни кубического уравнения: 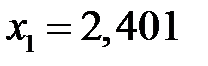; ; 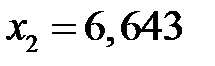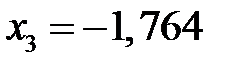. Подходит только корень 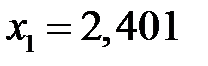. Значение функции прогибов в точке экстремум 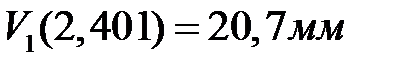(вычислено раннее).

Данное исследование необходимо, если требуется проверить условие жесткости, когда величина допустимого прогиба задана.