Перемещения и деформации.

Под действием внешних сил тело деформируется, т.е. изменяет свои размеры и форму (рис.2.9). Некоторая произвольная точка M переходит в новое положение M_1. Полное перемещение MM₁ будем разлагать на компоненты u, v, w , параллельные осям координат.

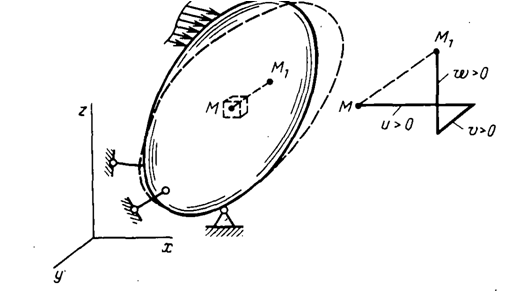
Рис 2.9 Полное перемещение точки и его компоненты.

Но перемещение данной точки еще не характеризует степень деформирования элемента материала у этой точки (пример:человек висит на канате, часть каната ниже захвата не деформируется).

Введем понятие деформаций в точке как количественную меру деформирования материала в её окрестности.Выделим в окрестности т. М элементарный параллелепипед 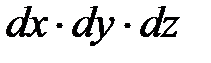(рис. 2.10). За счет деформации длины его ребер получат удлинение .

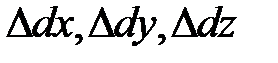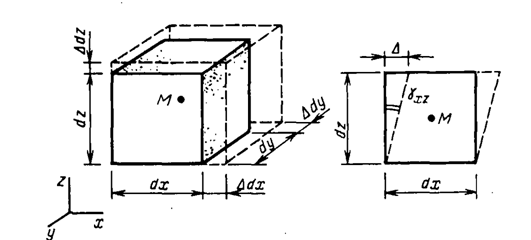
Рис 2.10 Линейная и угловая деформации элемента материала.

Линейные относительные деформации в точке определятся так ( ):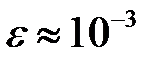

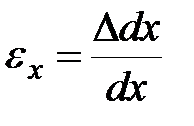
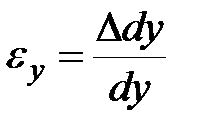
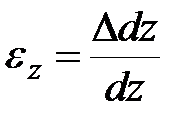
(2.5)

Кроме линейных деформаций возникают угловые деформации или углы сдвига, представляющие малые изменения первоначально прямых углов параллелепипеда(например, в плоскости 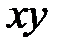это будет 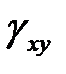). Углы сдвига весьма малы и имеют порядок .

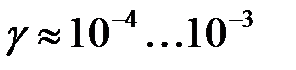Введенные относительные деформации в точке сведем в матрицу

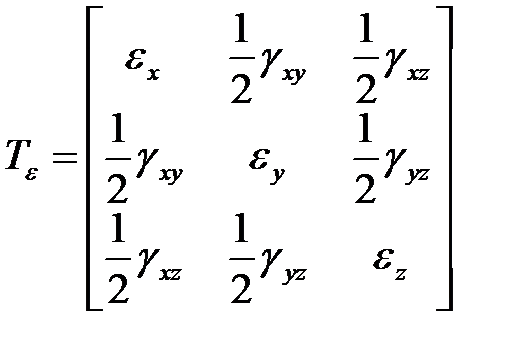. (2.6)

Величины (2.6) количественно определяют деформацию материала в окрестности точки и составляют тензор деформаций.