Относительное изменение объема параллелепипеда.
Относительное изменение объема параллелепипеда 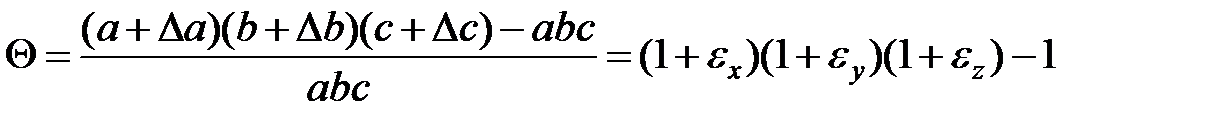 .
.
Раскрываем скобки и отбрасываем слагаемые 2-го и 3-го порядков малости
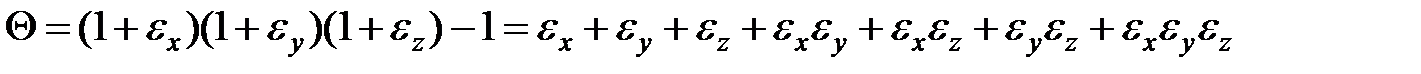 .
.
В результате получаем
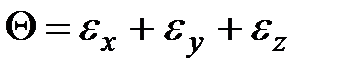 . .
| (3.14) |
Выразим через нормальные напряжения. Подставим относительные деформации (3.12) в (3.14) в результате получим:
через нормальные напряжения. Подставим относительные деформации (3.12) в (3.14) в результате получим:
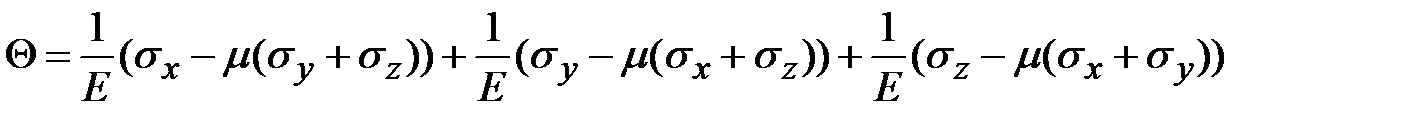 . После несложных преобразований будем иметь
. После несложных преобразований будем иметь
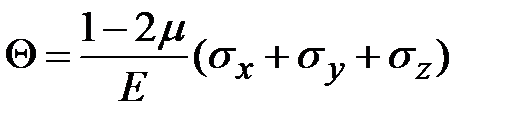
| ( 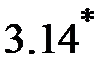 ) )
|
Используя формулу ( 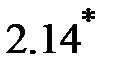 ) можно показать, что коэффициент Пуассона для различных материалов может изменяться в диапазоне
) можно показать, что коэффициент Пуассона для различных материалов может изменяться в диапазоне 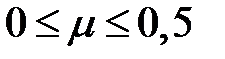 .
.
3.7 Напряжения в сечениях, наклонных к оси стержня, при растяжении и сжатии.
Рассмотрим стержень, растянутый равномерно распределенной нагрузкой интенсивностью σ ( рис.3.17 а) Рассечем стержень по наклонному сечению и отбросим правую часть ( рис.3.17 б)
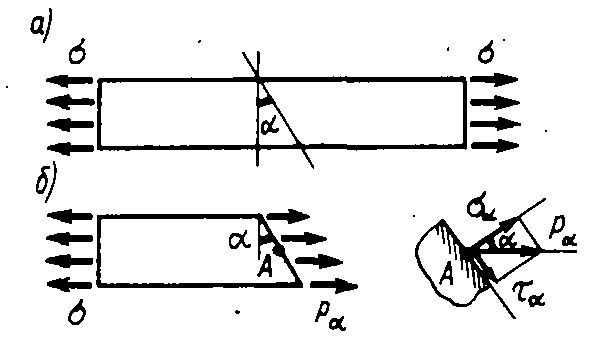
Рис. 3.17 Напряжения на наклонных площадках растянутого стержня.
На наклонной площадке полные напряжения 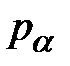 будут направлены вдоль продольной оси и распределены равномерно (все волокна растянуты одинаково (ЧЦР)). Оставшаяся левая часть стержня находится в равновесии:
будут направлены вдоль продольной оси и распределены равномерно (все волокна растянуты одинаково (ЧЦР)). Оставшаяся левая часть стержня находится в равновесии:
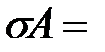 p p 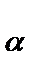 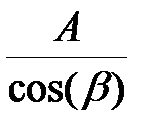 , ,
| 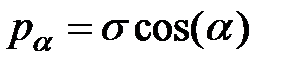 , ,
| 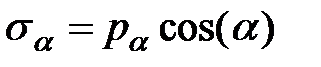 , ,
| 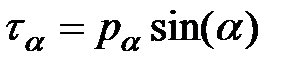 . .
|
Нормальные и касательные напряжения в наклонном сечении:
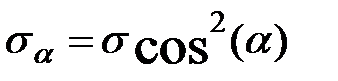
| 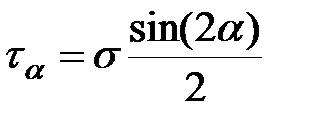
| (3.15) |
На площадках совпадающих с поперечным сечение (α=0)
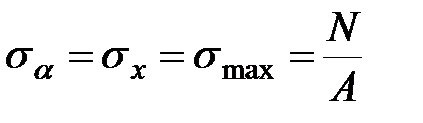
| 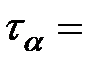 0 0
| (3.16) |
На площадках наклоненных под углом α= 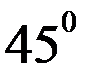
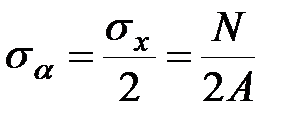
| 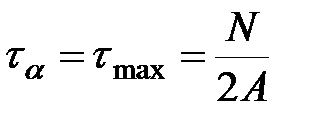
| (3.17) |
На продольных площадках ( вдоль оси стержня) (α= 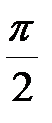 )
)
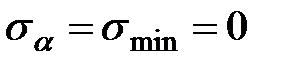
| 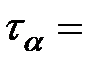 0 0
| (3.18) |
Варианты действия напряжений показаны на рис. 3.18
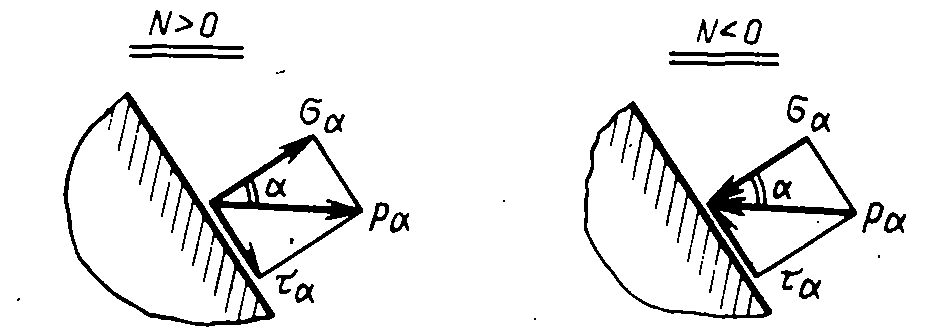
Рис. 3.18 Варианты действия напряжений 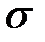
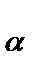 ,
, 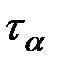 .
.
На двух взаимно перпендикулярных площадках касательные напряжения равны по абсолютной величине
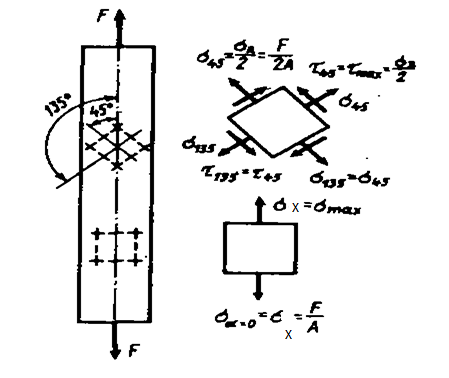
Рис. 3.19 Нормальные и касательные напряжения на гранях выделенных элементов
Дата добавления: 2017-09-01; просмотров: 1568;











