Определение перемещений в общем случае растяжения и сжатия.

Рассмотрим стержень, нагруженный на правом конце равномерно распределенной нагрузкой интенсивностью 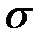, которая вызывает его растяжение (рис.3.8)

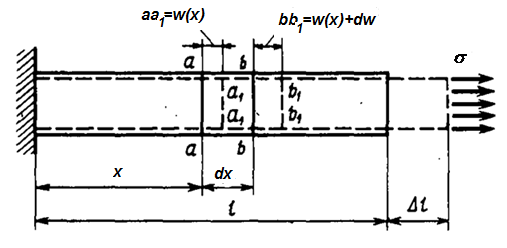
Рис. 3.8 Перемещения сечений а-а и b-b в растянутом стержне

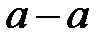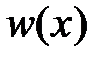Перемещение сечение равно . Сечение 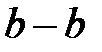отстоит от сечения 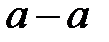на 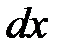, следовательно, его перемещение равно: 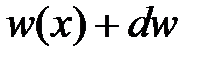. Таким образом, абсолютное удлинение участка 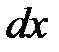равно: 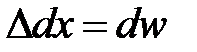. Относительная деформация участка длиной 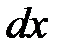равна: .

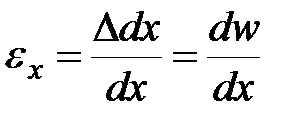Производная от продольного перемещения равна относительной деформации:

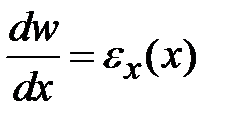
(3.6)

С учетом формул (3.5) ,(3.1) выражение для относительной деформации можно записать в виде 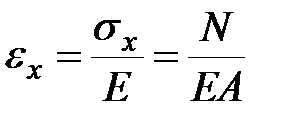. Таким образом, уравнение, связывающее перемещения и усилия примет вид

.

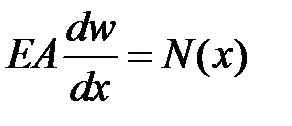(3.7)

Получим рабочие формулы для определения усилий и перемещений. Проинтегрируем обе части первого уравнения (3.2), в результате будем иметь

.

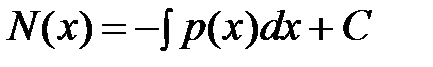(3.8)

Выражение для продольной силы подставим в (3.7) и проинтегрируем его обе части, получим

.

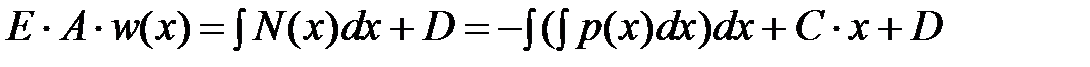(3.9)

Константы интегрирования и 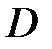в формулах (3.8), (3.9) определяют из статических и кинематических граничных условий (рис.3.9):

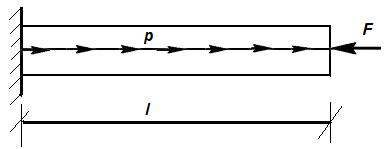Рис.3.9 Граничные условия

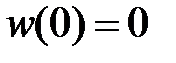Кинематическое условие ,   статическое условие .

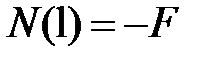Если на стержне распределенная нагрузка отсутствует ( 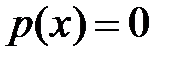), то уравнения (3.8), (3.9) принимают вид:

, .

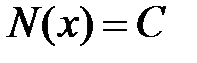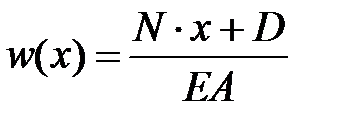(3.10)

Запишем уравнение равновесия элемента стержня в перемещениях. Для этого продифференцируем по 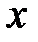обе части уравнения (3.7) и с учетом (3.2) получим:

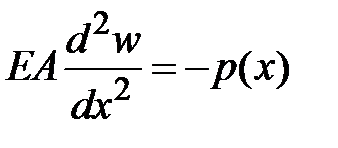
(3.11)

Отметим также, что полное удлинение стержня определяется по формуле (взаимное удаление или сближение концов стержня )

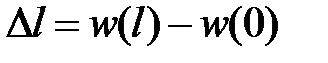
(3.12)

Правило знаков для продольных перемещений: положительным перемещениям соответствуют перемещения, совпадающие с положительным направлением оси х.

Приведем примеры решения задач с использованием полученных уравнений.

Пример 3.2 Построить эпюру продольных сил и продольных перемещений для стержня переменного сечения от действия собственного веса. Длина стержня . Поперечное сечение прямоугольник: высота сечения 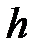, ширина меняется по длине от 0 до 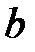. Объемный вес материала стержня .

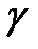г)

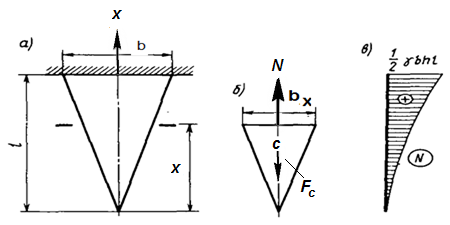
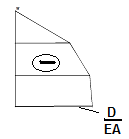
Рис. 3.6 Эпюры усилий и перемещений.

Из подобия треугольников (рис 3.6 а, б) 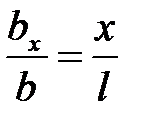находим ширину поперечного сечения стержня 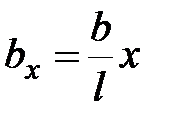в сечении с координатой 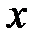. Уравнение равновесия отделенной части стержня (рис. 3.6 б) 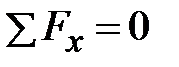, , 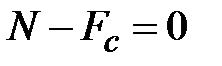или 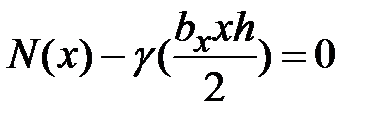. Закон

изменения продольной силы 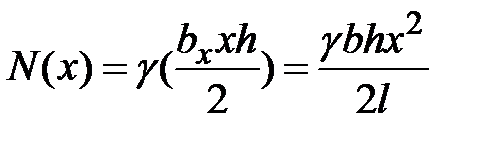- квадратная парабола: , , .

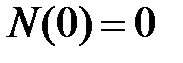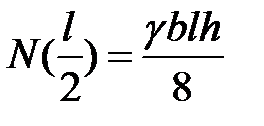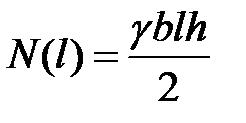Интенсивность распределенной нагрузки от сил собственного веса 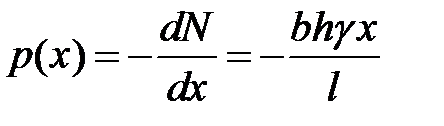- изменяется по линейному закону: , .

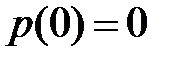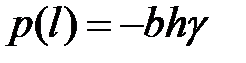Проверяем по формуле (3.8) 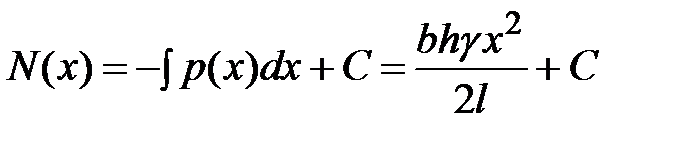. На свободном конце стержня продольная сила равна нулю 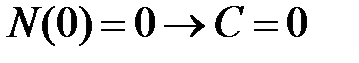. Тогда .

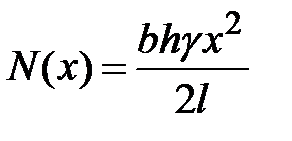Определим перемещения поперечных сечений по формуле (3.9).

.

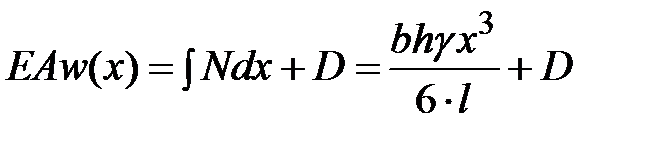Константу 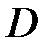найдем из условий закрепления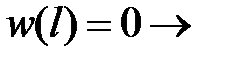 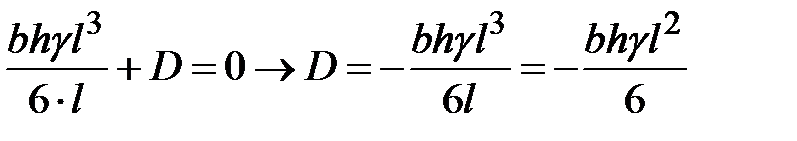.Тогда перемещение сеченийизменяются по длине стержня по закону кубической параболы .

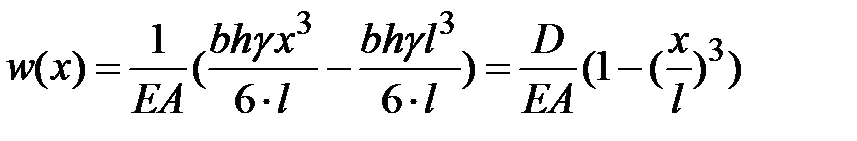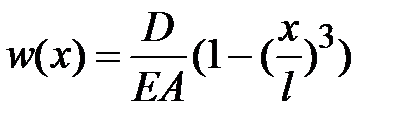
Строим эпюру по четырем точкам: , , , .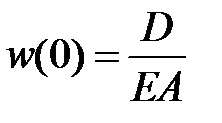

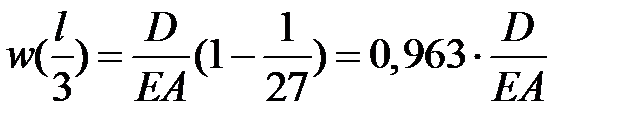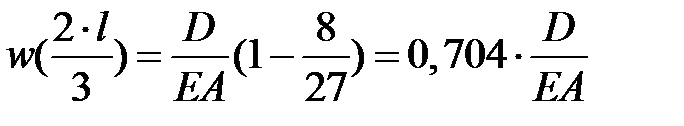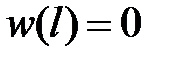Все ординаты эпюры продольных перемещений меньше нуля (D<0), т.к. сечения перемещаются против оси x.

Константа 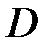пропорциональна перемещению поперечного сечения в начале координат.

Пример 3.3Для стержня, нагруженного как показано на рис. 3.11 а, построить эпюру продольных усилий 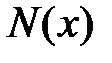и перемещений .

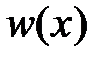Удаляем опорное устройство, 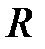- опорная реакция (рис. 3.11 б). Составляем уравнение равновесия .

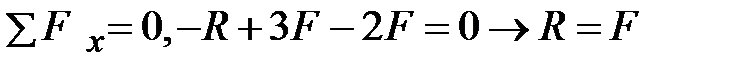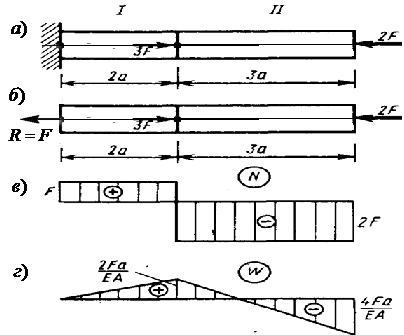
Рис.3.11 К примеру 3.3

Начало координат на левом конце стержня.

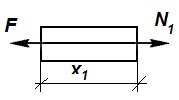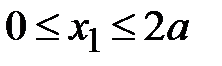
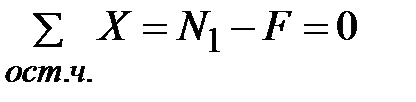Рис. 3.12 1-й участок 1-й участок.   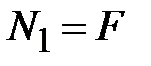Используем формулу (3.10) . .

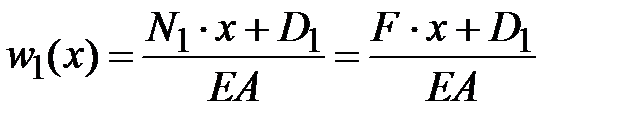
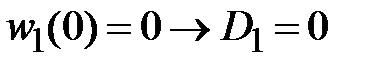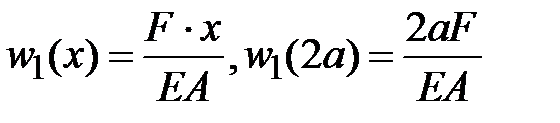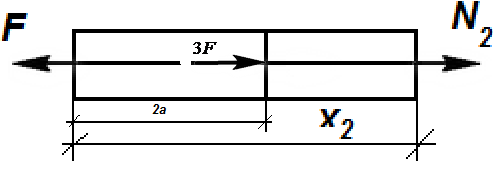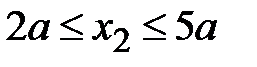
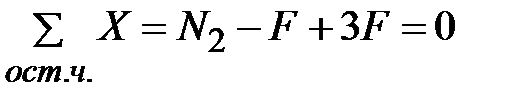Рис. 3.13 2-ой участок 2-й участок. 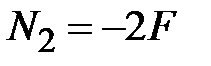Используем формулу (3.10) 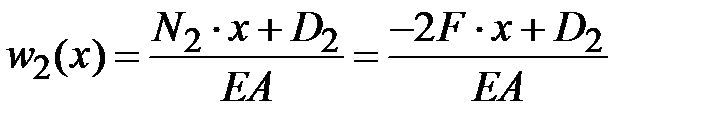Константу 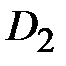определяем из условия непрерывности перемещений на границе участков . .

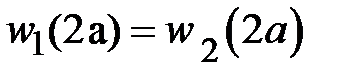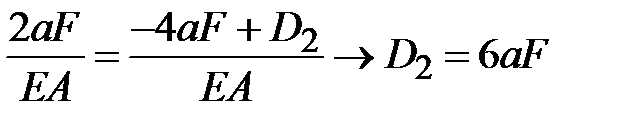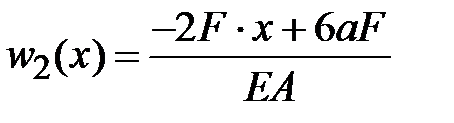
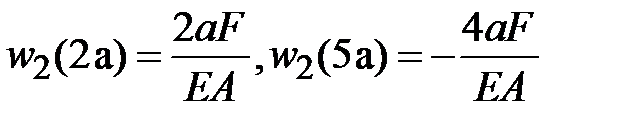
Пример 3.4Для стержня, нагруженного как показано на рис. 3.14 а, построить эпюру продольных сил 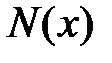и перемещений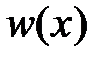

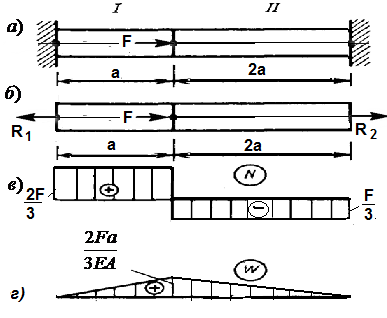
Рис. 3.14 Статически неопределимая задача

Удалим опорные устройства, а действие их на стержень заменим неизвестными реакциями 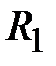, 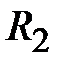.Составим уравнение равновесия (рис. 3.14 б)

, .

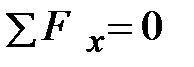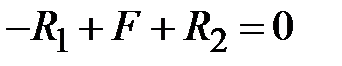Имеем одно уравнение и два неизвестных 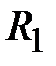, 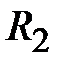. Уравнений статики недостаточно для определения всех неизвестных реакций. Такая задача называется статически неопределимой. Для ее решения удобно использовать уравнения (3.10).

1-й участок. 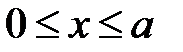. Записываем уравнения (3.10) на первом участке 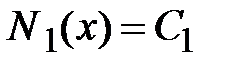, 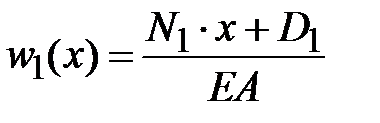. Перемещение поперечного сечения на левом конце стержня равно нулю , .

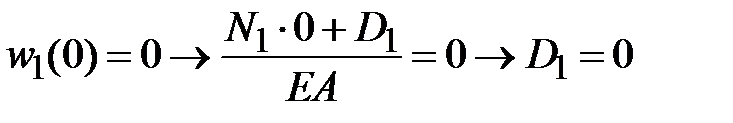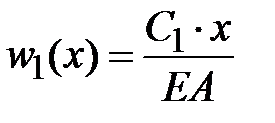2-й участок. 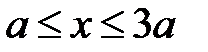. Записываем уравнения (3.10) на втором участке 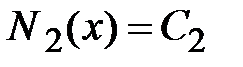, 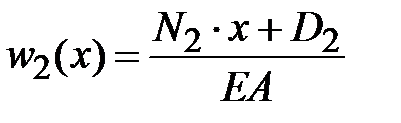. Перемещение поперечного сечения на правом конце стержня равно нулю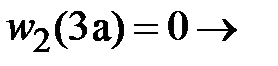 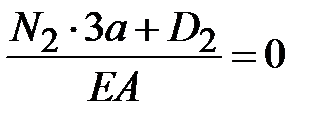или

( )

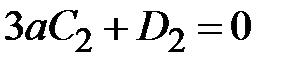
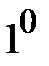Перемещения сечений на границе участков равны 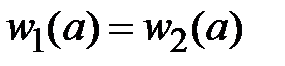, 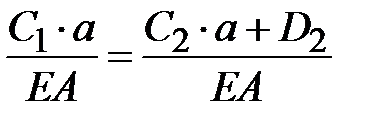или

( )

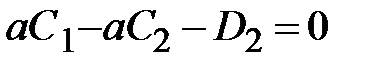
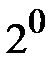Вырежем двумя близкими сечениями узел вблизи точки с координатой 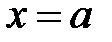и запишем уравнение равновесия

.

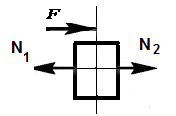
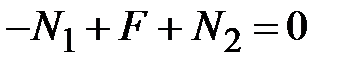Последнее уравнение примет вид

( )

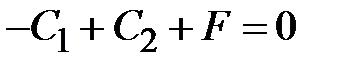
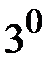Решаем систему уравнений ( 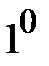)-( ) 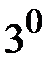относительно 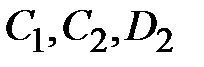. Умножаем ( 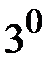) на 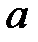и складываем с ( 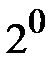) в результате получаем 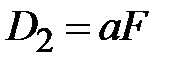. Из уравнения ( 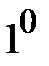) находим 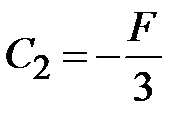. Подставляем 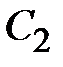в ( 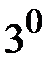) получаем .

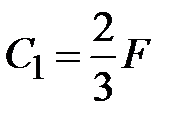Записываем окончательные выражения для усилий и перемещений на участках:

1-й участок. . , ;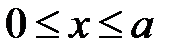

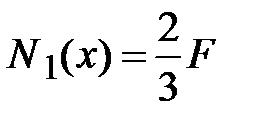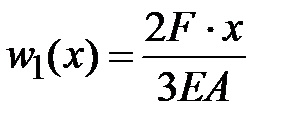2-й участок. . , .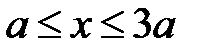

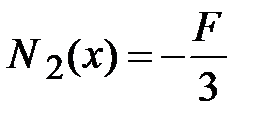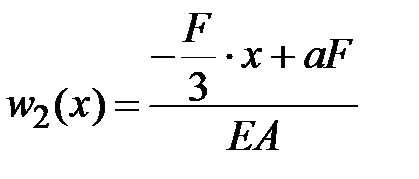Строим эпюры усилий и перемещений (рис.3.14 в ,г)

Реакции в опорных сечениях 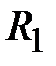, 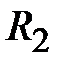находим из уравнений равновесия узлов:

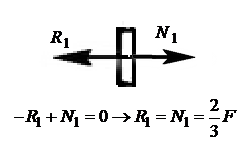
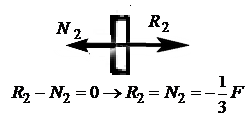
Таким образом, первоначальное направление 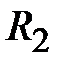надо заменить на противоположное (рис.3.14 б).

3.5 Обобщенный закон Гука.

Рассмотрим прямоугольный параллелепипед с ребрами единичной длины по граням которого действуют только нормальные напряжения .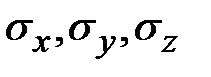

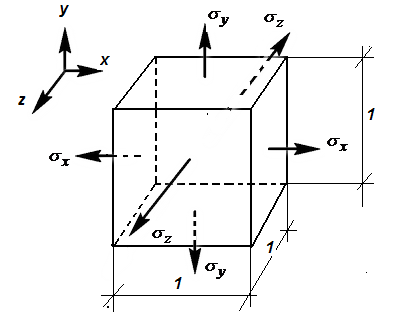
Рис 3.15 Трехосное растяжение элемента

Используем принцип независимости действия сил. Деформации элемента при растяжении его вдоль осей x,y,z равны (рис. 3.16):

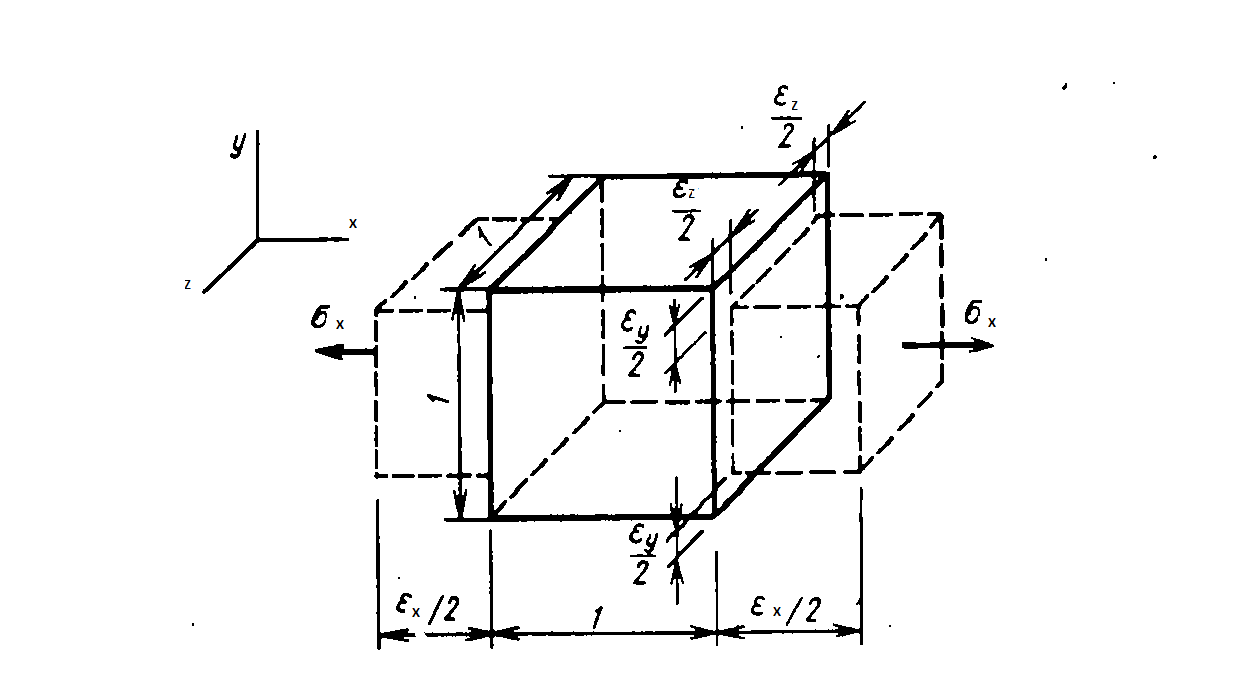
Рис. 3.16 Деформации элемента при растяжении его вдоль оси x.

вдоль оси x	,	,	;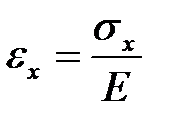
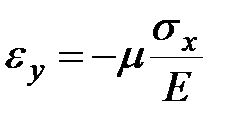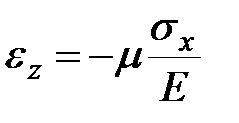вдоль оси y	,	,	;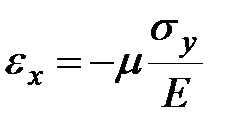
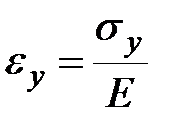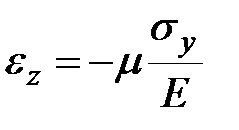вдоль в оси z	,	,	.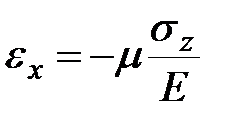

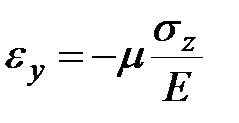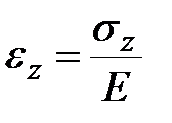Складываем правые части равенств по столбцам, получаем формулы обобщенного закона Гука. , ,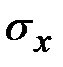

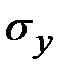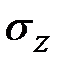
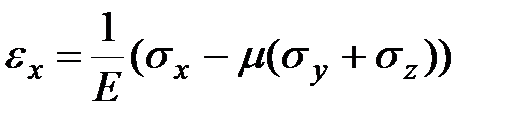
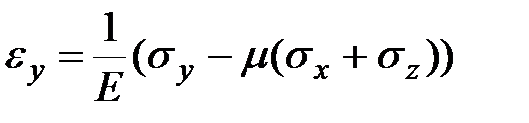
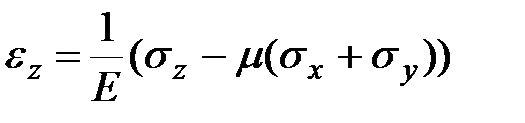
(3.13)