Дифференциальные зависимости между продольной силой и интенсивностью распределенной нагрузки.
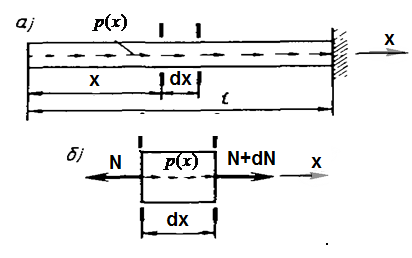

Рис. 3.5 Вывод дифференциальной зависимости между 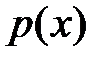 и
и 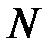 .
.
Обозначим 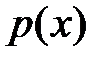 - интенсивность распределенной нагрузки, действующей на стержень. Тогда уравнение равновесия элемента
- интенсивность распределенной нагрузки, действующей на стержень. Тогда уравнение равновесия элемента 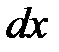 стержня (
стержня ( 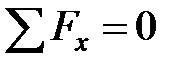 ) примет вид:
) примет вид: 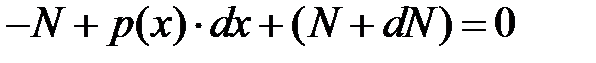 . В результате получаем искомую дифференциальную зависимостьмежду продольной силой и интенсивностью распределенной нагрузки
. В результате получаем искомую дифференциальную зависимостьмежду продольной силой и интенсивностью распределенной нагрузки
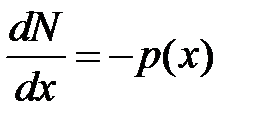 . .
| (3.2) |
3.3 Закон Гука при растяжении и сжатии.
Рассмотрим чистое центральное растяжение стержня силами интенсивностью 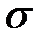 . Будем считать, что внешние силы вызывают в стержне только упругие деформации, т.е. после снятия нагрузки стержень принимает свою первоначальную форму и размеры.
. Будем считать, что внешние силы вызывают в стержне только упругие деформации, т.е. после снятия нагрузки стержень принимает свою первоначальную форму и размеры.

Рис. 3.7 Продольные и поперечные деформации стержня.
Введем обозначения:
| абсолютная продольная деформация | относительная продольная деформация | относительная поперечная деформация | относительная поперечная деформация |
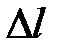
| 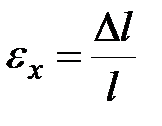
| 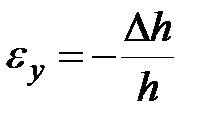
| 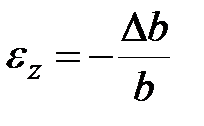
|
На основе серии опытов со стержнями из различных материалов были установлены следующие положения закона Гука:
1) абсолютное удлинение стержня прямо пропорционально продольной силе 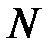 , длине
, длине  и обратно пропорционально площади поперечного сечения
и обратно пропорционально площади поперечного сечения 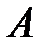 и модулю упругости материала стержня
и модулю упругости материала стержня 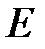
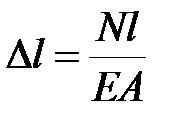 . .
| (3.3) |
2) относительная поперечная деформация прямо пропорциональна относительной продольной деформации
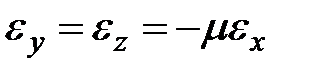
| (3.4) |
В формуле (3.4) 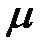 -коэффициент Пуассона, безразмерная величина. Знак минус в формуле (3.4) означает, что если в направлении оси
-коэффициент Пуассона, безразмерная величина. Знак минус в формуле (3.4) означает, что если в направлении оси 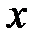 стержень испытывает деформации растяжения, то в направлении осей
стержень испытывает деформации растяжения, то в направлении осей 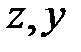 стержень испытывает деформации сжатия.
стержень испытывает деформации сжатия.
Таким образом, для каждого материала существует две упругие постоянные : 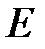 -модуль упругости и коэффициент Пуассона
-модуль упругости и коэффициент Пуассона 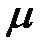 .
.
Если обе части формулы (3.3) разделить на  , а затем воспользоваться формулами для нормальных напряжений и относительных деформаций, то закона Гука можно записать в виде
, а затем воспользоваться формулами для нормальных напряжений и относительных деформаций, то закона Гука можно записать в виде

| (3.5) |
Из формулы (3.5) следует, что модуль упругости имеет туже размерность, что и напряжение, т.е. 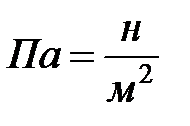 .Например, для прокатной стали
.Например, для прокатной стали 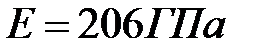 ,
, 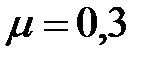 .
.
Дата добавления: 2017-09-01; просмотров: 1931;











