Напряженное состояние в точке

Рассмотрим тонкую пластинку, находящуюся под действием произвольной системы сил, приложенных к кромкам пластинки и лежащих в ее плоскости (рис. 5.1 а). На поверхности пластинки параллельной плоскости xy напряжения отсутствуют ( ). Так как толщина пластинки мала, то можно считать, что напряжений нет и внутри пластинки на площадках параллельных этой поверхности. Поэтому в точках пластинки в общем случае имеет место плоское напряженное состояние.

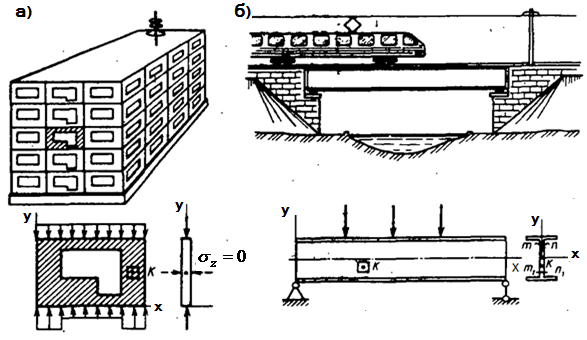
Рис. 5.1 Примеры плоского напряженного состояния:

панель сборного здания (а), стенка мостовой балки (б)

Вырежем элементарный параллелепипед из пластинок в окрестности произвольной точки сечениями, перпендикулярными плоскости пластинки. Со стороны среды, окружающий параллелепипед, на него действуют в общем случае как нормальные, так и касательные усилия.

На рис. 5.2 б показаны векторы нормальных и касательных напряжений, соответствующие этим усилиям. Оси координат совмещены с центром элемента точкой К.

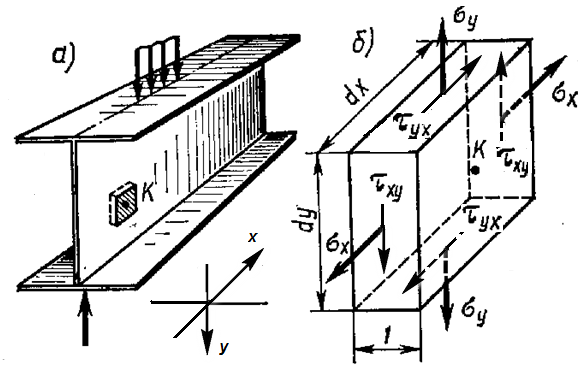
Рис. 5.2 Напряжения на гранях элемента в случае плоского напряженного состояния.

Напряженное состояние малого параллелепипеда является однородным. Это значит, что в любых его параллельных сечениях напряжения можно считать распределенными равномерно, а по величине одинаковыми. Поэтому компоненту элементарной силы на любой площадке получим как произведение напряжения на площадь площадки, например 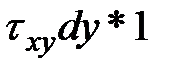или просто 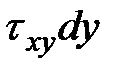. Будем считать, что напряжения, действующие по граням параллелепипеда: σ_x,σ_y,τ_xy известны (определяются в результате решения плоской задачи теории упругости).

Напряженным состоянием в точке называют совокупность напряжений, действующих по всевозможным площадкам, проведенным через эту точку.

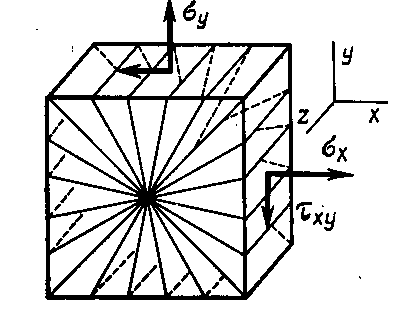
Рис. 5.3 Пучок площадок, проведенных через данную точку