Главные площадки и главные напряжения.

1 234

Выражение (5.5) показывает, что 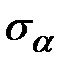является функцией угла наклона площадки α. Рассмотрим задачу об отыскании площадок, в которых возникают экстремальные для точки нормальные напряжения. Для этого найдем производную от (5.5) и приравняем её нулю:

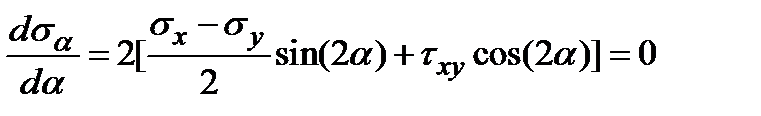
(5.9)

Сравнив выражение в квадратных скобках с формулой (5.7), можем равенство (5.9) переписать в эквивалентной форме:

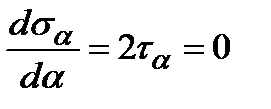
(5.10)

Из (5.10) следует, что на площадках где действуют экстремальные нормальные напряжения, касательные напряжения равны нулю. Такие площадки называются главными, а соответствующие им нормальные напряжения – главными напряжениями в точке.

Из выражения (5.9) получим тангенс двойного угла наклона нормалей главных площадок:

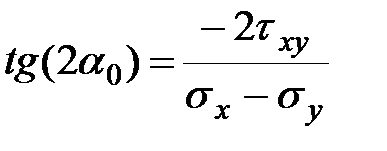
(5.11)

Выражение (5.11) дает два взаимно перпендикулярных направления с углам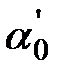и и 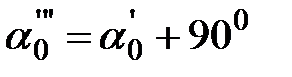, по которым действуют главные напряжения σ_max, σ_min.

Для определения значений главных напряжений подставим в формулу (5.5) α=α₀(α_0-определено из решения уравнения). После преобразований (см. стр. 348, 349 учебник «Сопротивление материалов» А.В. Александров, В.Д. Потапов, Б.П. Державин.) получим:

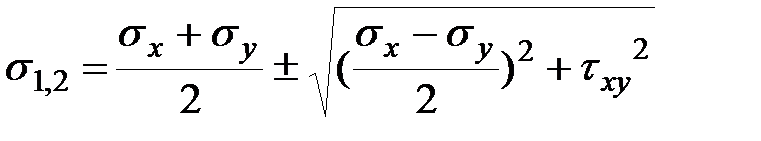
(5.12)

В этой формуле знак плюс соответствует максимальному главному напряжению, а минус – минимальному. Очевидно, что

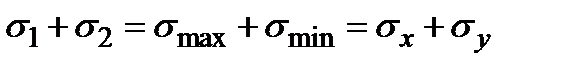
(5.13)

Из приведенного вывода следует, что при любых исходных напряжениях σ_x,σ_y,τ_xy в данной точке существует параллелепипед, на гранях которого действуют только нормальные напряжения.

Приведем формулу для тангенса одиночного угла наклона искомой главной площадки, на которой действует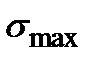

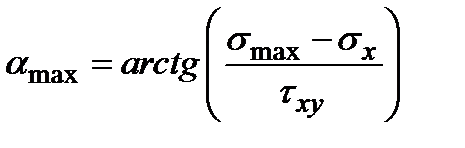. (5.14)

В формуле (5.14) положительный угол отсчитывается от оси 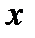по ходу часовой стрелки.

Угол между осью 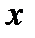и внешней нормалью к сечению, в котором действует 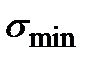определяется по формуле .

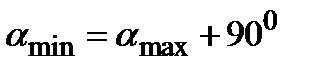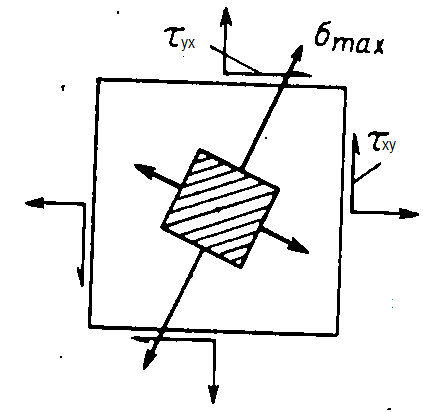
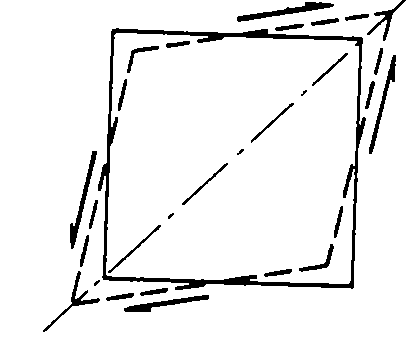
Простое универсальное правило для направления 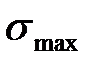. Направление σ_max всегда проходит через те две четверти осей координат, к которым сходятся стрелки касательных напряжений τ_xy,и τ_yx (см. рис. 5.6)

Рис. 5.6 Направление σ_max

1 234

Дата добавления: 2017-09-01; просмотров: 1484;