Напряжения в наклонных площадках.

Разрежем параллелепипед, изображенный на рис.5.2 б, наклонным сечением, выделив из него треугольную призму (рис. 5.4 а)

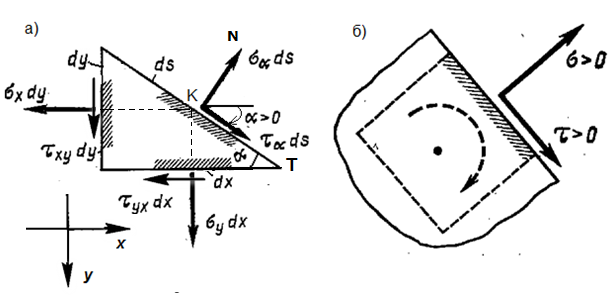
Рис. 5.4 Элементарная призма и напряжения на ее гранях-площадках (а), правило знаков для напряжений (б).

Угол между осью x и внешней нормалью N к наклонной грани считаем положительным (α>0), если он отсчитывается по ходу часовой стрелки. На гранях пластинки показаны нормальные и касательные усилия (толщина пластины δ=1). Составим уравнение: сумма моментов всех сил относительно точки K (т.K -середина гипотенузы)

.

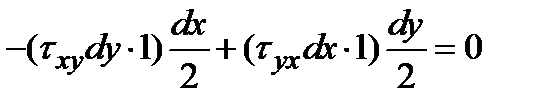(5.1)

Из уравнения (5.1) получим численное равенство закона парности касательных напряжений

=

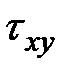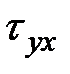
(5.2)

Вблизи прямого угла касательные напряжения равны по модулю и направлены так, что либо сходятся к вершине прямого угла, либо расходятся от неё.

Определим напряжения на наклонной грани. При определении напряжений на наклонной площадке будем придерживаться правила знаков, показанного на рис. 5.4 б: нормальное растягивающее напряжение считается положительное; касательное напряжение положительно, если его вектор вращает элемент по ходу часовой стрелки. Согласно этому правилу знаков, показанные напряжения на рис. 5.5 τ_xy<0, τ_yx>0.

Для определения напряжений 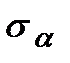, 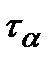спроектируем все силы на оси KN и KT (рис.5.5).

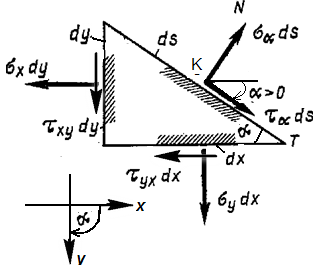
Рис. 5.5 Треугольная пластинка и напряжения на ее гранях

Сумма проекций всех сил на ось KN:

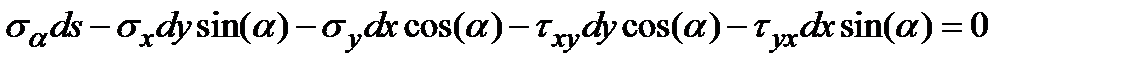
Разделим уравнение (5.3) на ds и с учетом:

,

,

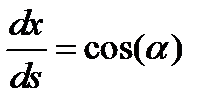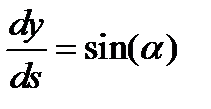(5.4)

получим выражение для σ_α

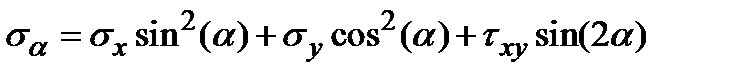
(5.5)

Сумма проекций всех сил на ось KТ:

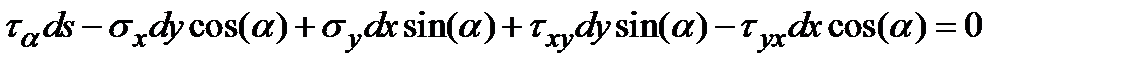
(5.6)

Разделим уравнение (5.6) на ds и с учетом (5.4) и (5.2) получим:

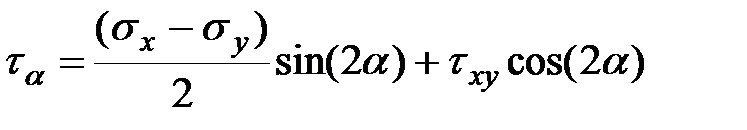
(5.7)

Сумма нормальных напряжений на взаимно ортогональных площадках не зависит от угла α (инвариантна к направлением осей координат) и, следовательно, для данной точки эта сумма постоянна:

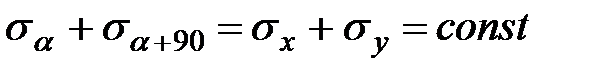
(5.8)