Использование линий влияния для определения усилий в заданном сечении от системы сосредоточенных и распределенных неподвижных нагрузок

Как известно, задачи такого рода успешно решаются методами, изучаемыми в курсе сопротивления материалов. Однако с помощью линии влияния в ряде случаев такие решения находятся гораздо проще и быстрее, особенно тогда, когда количество сосредоточенных распределенных нагрузок велико.

Расчет производится на основе следующих соображений. Предположим, что требуется определить какое-либо усилие S (это может быть изгибающий момент М, перерезывающая сила Q или продольная сила N) в заданном сечении балки от произвольной системы неподвижных нагрузок.

Построим линию влияния для изменения определяемого усилия в заданном сечении. Допустим, что кривая на рис. 9.7 и есть эта лини: влияния, тогда ординаты линии влияния у₁, у₂ и у_п выражают величину усилия в исследуемом сечении от единичного груза, стоящего над соответствующей ординатой.

Если над данной ординатой у₁ стоит не единичный груз, а груз Р₁ то усилие в исследуемом сечении будет от груза Р₁ – y₁Р₁, от груза Р₂ – у₂Р₂, от груза Р_п – У„Р_п. Подобные рассуждения справедливы для любого количества сосредоточенных сил. Распределенную нагрузку можно представить как совокупность элементарных сосредоточенных сил qdx. Каждая элементарная сила вызывает в исследуемом сечении усилие y_xqdx, причем, для равномерно распределенной нагрузки q = const, а для треугольной распределенной нагрузки интенсивность ее зависит от х.

Общее усилие в исследуемом сечении от любой системы нагрузок равно сумме усилий от отдельных сосредоточенных сил и распределенных нагрузок, т. е.

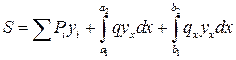. (9.9)

Учитывая, что

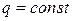, а ,

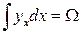где 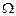– площадь, ограниченная линией влияния и расположенная под распределенной нагрузкой (на рис. 9.7 заштрихована), упрощаем выражение для усилия

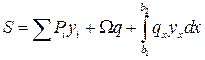(9.10)

В большинстве случаев можно пользоваться формулой с двумя первыми членами, так как в практике редко встречаются нагрузки, распределенные по сложному закону

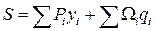. (9.11)

Пример

Определить с помощью линий влияния изгибающий момент посредине пролета балки от системы нагрузок (рис. 9.8). Правильность решения проверить обычными методами сопротивления материалов.

Решение. Строим линию влияния М_{а = 2} для сечения посредине пролета. Под левой опорой откладываем а = 2 м. Из подобия треугольников определяем у₁ = -0,5 м; у₂ = 1 м; у₃ = 0,5 м. Находим площади

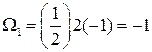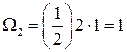м²;

м².

Общее усилие

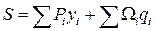
Изгибающий момент (тс∙м)

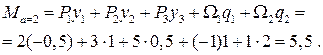
Проверяем полученное значение изгибающего момента посредине пролета М_{а = 2}, которое проще найти, взяв сумму моментов всех сил справа от рассматриваемого сечения.

Определяем сумму моментов всех сил относительно точки А

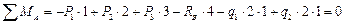
Откуда найдем реакцию (тс)

.

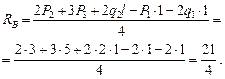Теперь находим изгибающий момент, учитывая, что рассматриваем равновесие правой части и пользуемся обратным правилом знаков

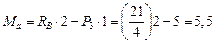тс∙м.

Контрольные вопросы к лекции № 9

1. Что называется линией влияния опорной реакции, изгибающего момента, поперечной силы?

2. Что называется линией влияния прогиба?

3. Какую размерность имеет линия влияния реакции, поперечной силы, момента?

4. Для скольких сечений балки возможно построение линии влияния?

5. Всегда ли линии влияния изгибающих моментов в двухопорной балке имеют треугольное очертание с вершиной под сечением и почему?

6. Какой вид имеет линия влияния реакции, если балка имеет одну консоль?

7. То же, две консоли?

8. Можно ли строить линию влияния от двух грузов и рационально ли это?

9. Можно ли строить линию влияния от пары с моментом М = 1?

10. Как используется построенная линия влияния (A, Q, М) для определения соответствующего усилия при загружении всей балки равномерной нагрузкой?