Методика построения линий влияния

Линией влияния (инфлюэнтной линией) называется график изменения усилий в данном сечении или элементе в зависимости от положения единичного груза на конструкции.

Линии влияния могут быть построены экспериментально или аналитически на основе положений теоретической механики.

Построим линии влияния опорных реакций Ra и Rb обычной балки на двух опорах (рис. 9.1). На опоре В установим динамометр и будем перемещать единичный груз по балке от А к Б. Когда груз стоит над опорой А и полностью передается на нее, реакция Rb равна нулю. По мере перемещения единичного груза вправо большая часть его передается на опору В и, когда груз станет точно над опорой В, опорная реакция R_B будет равна единицы.

Чтобы построить линии влияния опорных реакций R_B и R_A аналитическим путём, напишем уравнение зависимости R_A и R_B от х.

Сумма моментов всех сил относительно точки А

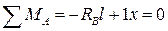, (9.1)

откуда

;

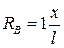При х = 0

;

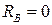При х = l

.

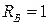Сумма моментов всех сил относительно точки В

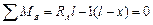, (9.2)

откуда

;

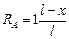при х = 0

;

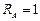при х = l

.

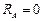В обоих случаях уравнение линии влияния содержит х только в первой степени, т. е. линии влияния представляют собой прямые (рис. 9.1).

Примечания:

1. Ординаты линии влияния у₁ и у₂ представляют собой в масштабе величины усилий (в данном случае опорной реакции) в одном и том же сечении или элементе, для которого построена линия влияния, при различном положении единичного груза на конструкции (над ординатой).

2. Ординаты линии влияния опорных реакций перерезывающих и других сил представляют собой безразмерную величину.

Построим линии влияния изгибающего момента М_а в сечении х = а балки на двух опорах (рис. 9.2). В зависимости от положения единичного груза на балке рассмотрим два случая:

Единичный груз находится справа от исследуемого сечения х = а. Рассматриваем равновесие левой части. Положительными считаем силы, направленные вверх, и момент по часовой стрелке:

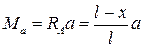; (9.3)

при х = 0

;

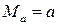при х = l

.

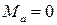Это уравнение правой ветви линии влияния момента справедливо только для области х ≥ а.

2. Единичный груз находится слева от исследуемого сечения х = а. Рассматриваем равновесие правой части. Применяем обратное правило знаков. Положительными считаем силы, направленные вниз, и момент против часовой стрелки:

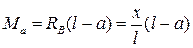; (9.4)

При х = 0 ;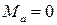

При х = l .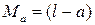

Уравнение левой ветви линии влияния действительно только при грузе слева, т. е. при х ≤ а.

Действительные участки ветвей линии влияния на рис. 9.2 отмечены более толстой линией.

Примечания:

1. Ветви линии влияния изгибающего момента в балке на двух опорах всегда пересекаются под исследуемым сечением.

2. Ординаты линии влияния М_а для балки на двух опорах имеют максимум под исследуемым сечением.

3. Построение линии влияния М_а можно начинать с откладывания в масштабе ординаты а под левой опорой, затем через вершину ординаты и нуль над опорой В провести правую ветвь, снести на нее положение исследуемого сечения; через найденную точку и нуль под опорой А провести левую ветвь, отделить действительные участки ветвей линии влияния.

4. Ординаты линии влияния изгибающего момента измеряются в сантиметрах, а площадь, ограниченная линией влияния,– в квадратных сантиметрах.

Построим линии влияния перерезывающей силы в сечении х = а балки на двух опорах (рис. 9.3). Груз находится справа от сечения х = а. Рассмотрим равновесие левой части (прямое правило знаков):

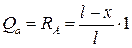; (9.5)

При х = 0

;

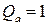При х = l

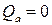
Груз находится слева от сечения х = а. Рассмотрим равновесие правой части (пользуемся обратным правилом знаков):

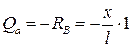; (9.6)

При х = 0

;

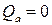При х = l

.

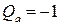После выделения действительных участков на ветвях линия влияния приобретает вид, показанный на рис. 9.3.

Примечания:

1. Ординаты линии влияния перерезывающей силы так же, как и опорной реакции, являются безразмерной величиной.

2. Площадь, ограниченная линией влияния перерезывающей силы, выражается в квадратных сантиметрах.

Построим линии влияния Ми Q в опорном сечении консольной балки с заделкой (рис. 9.4). Момент в опорном сечении

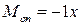; (9.7)

при х = 0

;

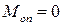при х = l .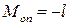

Перерезывающая сила в опорном сечении Q_oп (обратное правило знаков)

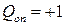. (9.8)

Линия влияния в данном случае не зависит от х, т. е. выражается прямой Q = 1, параллельной оси х (рис. 9.4).

Построим линии влияния для М_а и Q_a в произвольном сечении а консольной балки с заделкой (рис. 9.5). Груз находится слева от сечения а. Где бы ни стоял единичный груз слева от исследуемого сечения М_а = 0, т. е. левая ветвь линии влияния совпадает с осью х – нулевой линией отсчета.

При грузе справа

;

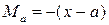при х = 0

;

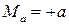при х = l ;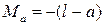

при х = а

.

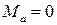Это уравнение линии влияния составлено при условии, что груз находится справа от исследуемого сечения, поэтому правая ветвь линии влияния действительна только при х ≥ а.

Чтобы построить линии влияния перерезывающей силы в сечении а, необходимо найти две ее ветви – правую и левую.

Груз находится слева от сечения а, перерезывающей силы в сечении а нет

.

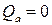Груз находится справа от сечения а (равновесие правой части, обратное правило знаков)

.

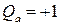После отделения действительных частей на ветвях линии влияния она получит вид, показанный на рис. 9.5.

Анализ уравнений, описывающих линии влияния для балок на двух опорах, показывает, что они не изменяются, если к балкам пристроить консоли. Линия влияния проходит над опорой, не изменяя своего направления.

Примеры линий влияния для двухопорных балок с консолями приведены на рис. 9.6.