Расчет тонких оболочек вращения по безмоментной теории

Листовые конструкции представляют собой тонкостенные оболочки с криволинейной или плоской поверхностью (пластинки).

Точный расчет листовых конструкций должен учитывать возможность существования в них объемно-напряженного состояния металла, возникающего под действием сосредоточенных и распределенных сил, а также изгибающих моментов. Такие расчеты достаточно сложны. Для расчета тонкостенных оболочек во многих случаях можно пренебрегать влиянием изгибающих моментов, считать напряжения от изгиба и кручения малыми. Схемы расчета и расчетные выражения при этом существенно упрощаются.

Экспериментальная проверка и данные практики эксплуатации листовых конструкций показывают, что применение расчета по безмоментной теории допустимо, если

,

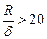где R – минимальный радиус кривизны;

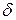,– толщина оболочки;

,

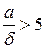где а – минимальный размер пластинки в плоскости.

Изгибающие моменты и объемные напряжения необходимо учитывать при расчете конструкций в местах приложения сосредоточенных сил, в местах концентрации напряжений (в углах пересечения поверхностей оболочек, в местах изменения толщины листов). Эти напряжения – местные, и для ослабления влияния их на прочность конструкции делают местные подкрепления. Толщину основных листов назначают без учета этих дополнительных напряжений.

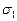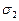В общем случае оболочка любой формы имеет два радиуса кривизны R₁ и R₂ во взаимно перпендикулярных плоскостях (рис. 10.1а). Центры этих радиусов обязательно лежат на нормали п, проведенной через точку О. Если внутри оболочки действует давление р, то нормальные напряжения, возникающие во взаимно перпендикулярных сечениях оболочки и , могут быть найдены из следующих соображений.

Рассмотрим равновесие произвольно выбранного бесконечно малого элемента со сторонами dS₁ dS₂ (рис. 10.1б). Возьмем сумму проекций всех сил, действующих на элемент, на нормаль п. Поскольку элемент находится в равновесии, то эта сумма равна нулю. Предварительно запишем следующие выражения:

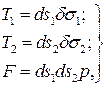, (10.1)

где 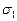и 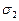– нормальные напряжения;

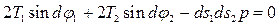. (10.2)

Ввиду малого значения углов 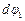и 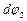будет справедливо

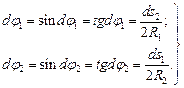(10.3)

Подставив выражения (10.1) и (10.3) в формулу (10.2), получим

.

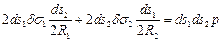Произведя сокращения и поделив все члены равенства на 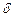, окончательно получим

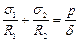. (10.4)

Обратим внимание, что радиус кривизны берется в той же плоскости, в которой расположен вектор соответствующего напряжения (рис. 10.1б).

Выражение (10.16), называемое уравнением Лапласа, содержит два неизвестных, поэтому для нахождения 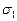и 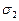его в общем случае недостаточно. Второе уравнение может быть получено из рассмотрения равновесия данной части оболочки, отсеченной плоскостью О, перпендикулярной к оси zz. Пересечение поверхности оболочки вращения с плоскостью происходит по окружности с радиусом r. Взяв сумму проекций всех сил на ось zz и имея в виду, что ∑Р_г = 0, получим

;

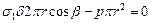При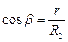

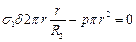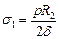; .(10.5)

Подставив 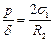из формулы (10.5) в уравнение (10.4), найдем соотношение 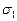и 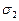через радиусы кривизны:

; ;

.

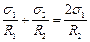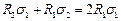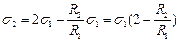Уравнение Лапласа позволяет в ряде случаев легко получить вышеприведенные зависимости для некоторых конкретных форм оболочки.

Сферическая оболочка. Для сферы характерно следующее:

; .

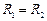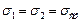Подставив эти значения в формулу (10.4), получим

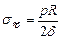.(10.6)

Цилиндрическая оболочка. Для цилиндра характерно следующее:

; .

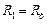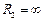Подставив эти значения в формулу (10.4), получим

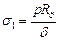. (10.7)

Полученные напряжения – это напряжения в продольном сечении цилиндрической обечайки или в продольном стыковом шве.

Напряжения в кольцевых сечениях или швах находят из следующих соображений (рис. 10.2а). Суммарная сила давления, действующая на днище и отрывающая его от цилиндрической части,

.

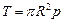Площадь кольцевого сечения, на которую распределяется сила Т,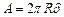 ,а нормальное напряжение в кольцевом сечении цилиндрической оболочки

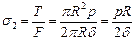. (10.8)

Сравнив выражение (10.8) с формулой (10.7), заметим, что нормальные напряжения в продольных сечениях или швах цилиндрической обечайки вдвое больше, чем в кольцевых. Для варианта кольцевых швов внахлестку (рис. 10.2б) из аналогичных рассуждений найдем касательные напряжения в шве

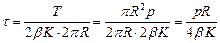.(10.9)

Расчеты других типов оболочек и сварных соединений подробно рассмотрены в источниках [1–5].

Контрольные вопросы к лекции № 10

1. Какие конструкции называют листовыми?

2. Как осуществляется процесс изготовления цилиндрической части и днища резервуаров? Какие напряжения при этом возникают?

3. Какие напряжения образуются в цилиндрической части? По какой формуле они определяются?

4. Как рассчитывают резервуары по методу предельного состояния?

5. Как назначают толщины днищ, лежащих на плотном основании?

6. Какие напряжения возникают в соединении цилиндра с днищем?

7. Как конструируют резервуары сферической формы?

8. Для чего днища резервуаров выполняют сферическими?

9. По какой формуле определяют напряжения в сферическом днище?

10. Как конструируют соединения сферического днища с цилиндрической частью, для чего ставят кольца жесткости?

11. Какие напряжения образуются в стенках горизонтальной цистерны при повышенном давлении в ее продольных и поперечных швах?