Проблемы поиска минимума в задачах с большим числом измерений.

Пусть в n-мерном векторном пространстве задана скалярная функция 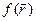. Наложим дополнительные условия 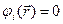, 1 ≤ i ≤ m; 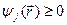, 1 ≤ j ≤ p. Условия типа равенств выделяют в пространстве некоторую (n – m)-мерную поверхность, а условия типа неравенств выделяют n-мерную область, ограниченную гиперповерхностями 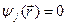. Число таких условий может быть произвольным. Следовательно, задача inf 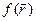есть поиск минимума функции n переменных в некоторой (n – m)-мерной области E. Функция может достигать минимального значения как внутри области, так и на ее границе. Однако перейти к (n – m)-мерной системе координат практически никогда не удается, поэтому спуск приходится вести во всем n-мерном пространстве.

Даже если нулевое приближение лежит в области E, естественная траектория спуска сразу выходит из этой области. Для принудительного возврата процесса в область E, например, используется метод штрафных функций: к 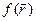прибавляются члены, равные нулю в E, и возрастающие при нарушении дополнительных условий (ограничений). Метод прост и универсален, однако считается недостаточно надежным. Более качественный результат дает использование симплекс-методов линейного программирования, однако данный вопрос в рамках настоящего курса не рассматривается.