И уравнениями выхода
МНОГОМЕРНЫЕ СИСТЕМЫ ПРИ ДЕТЕРМИНИРОВАННЫХ ВОЗДЕЙСТВИЯХ
1.2.1. Описание сигналов и систем
1. Описание сигналов. Входные, выходные и промежуточные детерминированные сигналы в многомерных системах представляются вектор-функциями времени, например:
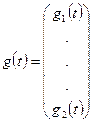 ,
, 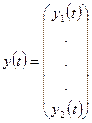 ,
,
где 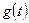 —
— 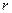 -мерный входной, a
-мерный входной, a 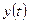 —
— 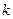 -мерный выходной сигналы. В качестве компонент входного сигнала
-мерный выходной сигналы. В качестве компонент входного сигнала 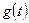 могут использоваться единичные ступенчатые функции (1.2) и дельта-функции (1.1).
могут использоваться единичные ступенчатые функции (1.2) и дельта-функции (1.1).
2. Описание систем. Многомерныелинейные нестационарные системы в отличие от одномерных имеют 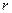 входов и
входов и 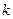 выходов (рис. 1.16). Они описываются уравнениями состояния вида
выходов (рис. 1.16). Они описываются уравнениями состояния вида
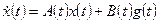 (1.35)
(1.35)
С начальными условиями
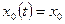 (1.36)
(1.36)
и уравнениями выхода
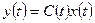 , (1.37)
, (1.37)
где 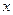 —
— 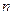 -мерный вектор состояния;
-мерный вектор состояния; 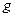 —
— 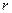 -мерный вектор входных воздействий (управлений);
-мерный вектор входных воздействий (управлений); 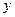 —
— 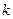 -мерный вектор выхода (вектор измерений);
-мерный вектор выхода (вектор измерений); 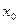 — начальное ан-тояние;
— начальное ан-тояние; 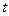 — время;
— время; 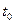 — начальный момент времени (момент подачи входного воздействия);
— начальный момент времени (момент подачи входного воздействия); 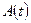 ,
, 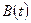 ,
, 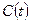 — матрицы размера
— матрицы размера 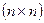 ,
, 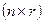 ,
, 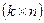 соответственно.
соответственно.
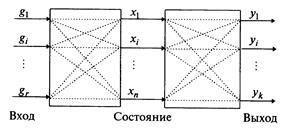
Рис. 1.16
Многомерную систему можно рассматривать как совокупность 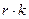 одномерных систем, каждая из которых связывает один из
одномерных систем, каждая из которых связывает один из 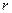 входов с одним из
входов с одним из 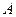 выходов. Если
выходов. Если 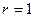 и
и 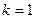 , система является одномерной. Если матрицы
, система является одномерной. Если матрицы 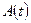 ,
, 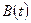 ,
, 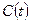 не зависят от времени
не зависят от времени 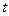 , система называется многомерной стационарной.
, система называется многомерной стационарной.
Пример 1.15. Записать уравнения состояния и выхода многомерной системы:
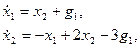
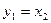
в матричной форме.
□ Определяем размерности сигналов: 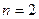 ,
, 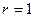 ,
, 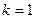 и записываем соответствующие уравнения:
и записываем соответствующие уравнения:
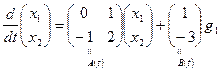 ,
, 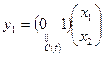 .
.
Пример 1.16. Записать уравнения состояния и выхода многомерной системы
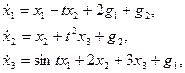
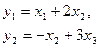
в матричной форме.
□ Определяем размерности сигналов: 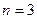 ,
, 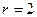 ,
, 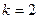 и записываем соответствующие уравнения:
и записываем соответствующие уравнения:
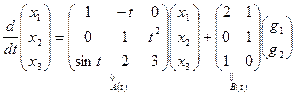 ,
, 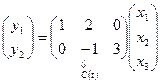 .
.
Пример 1.17. Записать уравнения состояния и выхода многомерной системы:
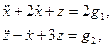
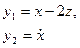
в матричной форме.
□ Обозначим 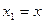 ,
, 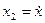 ,
, 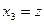 ,
, 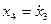 . Тогда уравнения можно переписать в виде
. Тогда уравнения можно переписать в виде
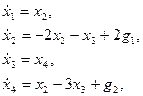
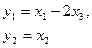
или в матричной форме ( 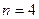 ,
, 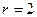 ,
, 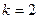 ):
):
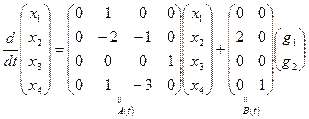 ,
, 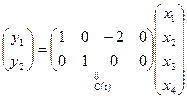 .
.
Дата добавления: 2017-09-01; просмотров: 1187;











