Связи вход-состояние и вход-выход

Рассмотрим многомерную линейную систему, описываемую уравнениями состояния и выхода:

, ,

.

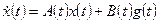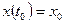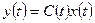Для линейных систем справедлив принцип суперпозиции: эффект, вызывае­мый суммой нескольких воздействий, равен сумме эффектов от каждого из воздействий в отдельности. Закон изменения вектора состояния линейной системы представляется в виде суммы свободного и вынужденного движений: 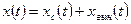. Аналогичное соотношение справедливо и для вектора выхо­да: 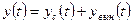в силу связи (1.37).

Свободное движение 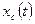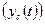происходит при отсутствии внешнего воздействия 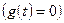вследствие ненулевых начальных условий (1.36). Оно опреде­ляется решением однородной системы уравнений, соответствующей исходному уравнению состояния (1.35):

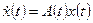(1.43)

с начальными условиями 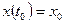. Если начальные условия нулевые, свободное движение в системе отсутствует, т.е. .

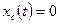Вынужденное движение 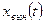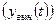— это реакция системы на внешнее воздействие 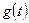при нулевых начальных условиях. Оно определяется решением неоднородного уравнения (1.35) при нулевых начальных условиях.

Для многомерных нестационарных систем, описываемых соотношениями (1.35) — (1.37), законы изменения векторов состояния и выхода определяются по формулам

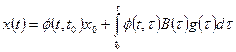, (1.44)

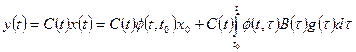, (1.45)

где 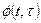— переходная матрица, или матрица Коши, являющаяся решением уравнения

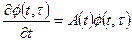(1.46)

начальным условием

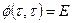. (1.47)

Первые слагаемые в (1.44), (1.45) описывают свободное движение, а вторые вынужденное.

Формулы (1.43) — (1.46) следуют из общего алгоритма решения линейных систем обыкновенных дифференциальных уравнений [40], включающего три этапа.

Первый этап. Решается однородная система дифференциальных уравнений

,

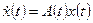соответствующая исходной неоднородной системе

.

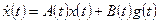Ее общее решение записывается в форме

,

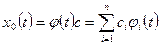где 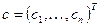вектор произвольных постоянных, 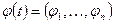— фундаментальная матрица, 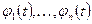линейно независимые решения однородной системы. Каждый столбец 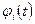(фундаментальной матрицы удовлетворяет одно­родной системе, т.е. справедливы равенства 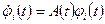, 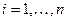или .

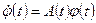Второй этап. Ищется общее решение неоднородной системы методом вариации произвольных постоянных:

,

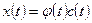где вектор-функция подлежит определению. Подставляя 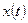в неоднородную систему, получаем

.

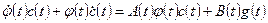С учето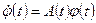м имеем

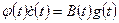или .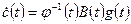

Обратная матрица 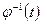существует, поскольку 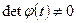как определитель Вронского. Интегрируя последнее соотношение, находим

,

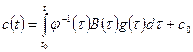где 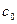— вектор произвольных постоянных. В результате искомое общее решение имеет вид

.

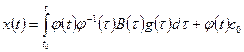Третий этап. Ищется частное решение неоднородной системы, удовлетворяющее начальным условиям :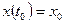

.

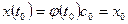Отсюда и

.

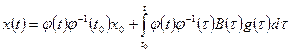Обозначая 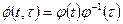, получаем формулу (1.44). При 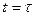получаем начальное условие (1.47). Умножая уравнение 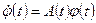справа на матрицу , имеем 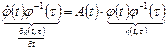, т.е. уравнение (1.46).

З а м е ч а н и е. Для многомерных стационарных систем, описываемых уравнениями

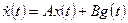, (1.48)

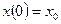, (1.49)

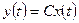, (1.50)

законы изменения вектора состояния и вектора выхода находятся по формулам

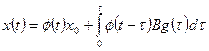, (1.51)

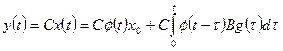, (1.52)

где 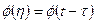— переходная матрица стационарной системы, зависящая от разности 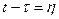. В данном случае решение уравнения (1.46) имеет вид

.