Вихревой характер магнитного поля.

Рассмотрим свойства магнитного поля в условиях магнитостатики. Эти условия предполагаются выполненными, если

- в рассматриваемой системе распределение электрического тока не меняется с течением времени;

- в рассматриваемой системе не происходит накопление или потеря электрического заряда.

В отличие от электростатики в условиях магнитостатики электрические заряды могут перемещаться в пространстве (электрический ток отличен от нуля), но специфическим образом в силу сформулированных выше условий. Важным необходимым свойством рассматриваемых систем является локальное условие отсутствия протекания электрического тока через замкнутую поверхность, ограничивающую конечную область пространства. Это возможно либо при обращении в нуль объёмной плотности тока, либо при обращении в нуль её нормальной составляющей на границе области.

В условиях магнитостатики из уравнения Пуассона для векторного потенциала магнитного поля (11) раздела 6.5 в вакууме (в среде с единичной магнитной проницаемостью)

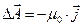(1)

следует второе фундаментальное свойство магнитного поля:

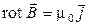. (2)

Действительно: 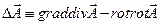, в условиях кулоновской калибровки векторного потенциала 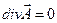, в силу определения векторного потенциала 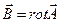. Уравнение (2) получено.

В силу математической теоремы Стокса получаем:

,

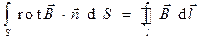а из определения силы тока 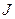через произвольную поверхность следует:

.

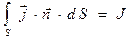Иными словами, циркуляция вектора магнитной индукции 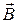по замкнутому контуру 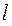, равна потоку вектора объемной плотности тока 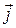через произвольную поверхность 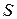, натянутую на этот контур, если направление обхода контура и направление нормали к поверхности 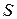согласованы между собой по правилу правого винта:

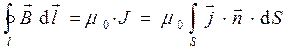. (3)

В элементарном изложении свойств магнитного поля в условиях магнитостатики рассматривают поле прямолинейного тока, текущего по бесконечному тонкому проводнику, величину рассчитывают с использованием закона Био-Савара-Лапласа и принципа суперпозиции, с учётом осевой симметрии для модуля вектора магнитной индукции получают выражение

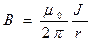. (4)

В итоге основное свойство магнитного поля в условиях магнитостатики (3) подтверждается в частном случае и постулируется его справедливость в остальных случаях.

Вспомним, что для вектора напряженности электростатического поля выполнялись локальное и интегральное условия потенциальности:

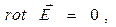
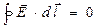. (5)

Условия потенциальности для вектора магнитной индукции в рассматриваемом общем случае не выполняются. Говорят, что магнитное поле является «вихревым».

Сравнивая между собой свойства вектора напряженности электростатического поля и вектора магнитной индукции в магнитостатическом случае, отметим, что соотношения (5) не предоставляют возможности выполнения практических расчётов величины напряженности поля даже в условиях высокой степени симметрии расположения электрических зарядов в пространстве, в то время как соотношения (3) в отдельных случаях позволяют рассчитать величину магнитной индукции в окрестности заданной системы стационарных токов.

Учитывая значимость уравнения (1) для теоретического описания стационарного магнитного поля, попытаемся доказать справедливость соотношения (1), исходя из интегральной формы закона Био-Савара-Лапласа.

Рассмотрим интегральную форму закона Био-Савара-Лапласа

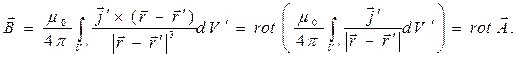
Легко видеть, что выражение для векторного потенциала магнитного поля можно записать в форме:

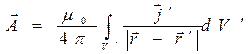. (6)

Непосредственное вычисление лапласиана по координатам точки наблюдения от выражения (6) приводит к последовательности результатов:

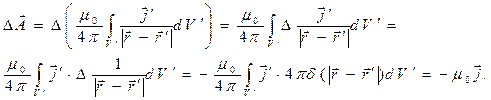
Здесь использовано предположение о возможности дифференцирования выражения (6) под знаком интеграла по координатам точки наблюдения, фундаментальное свойство функции 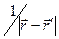и определение трёхмерной дельта-функции Дирака:

.

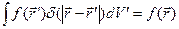Уравнение (1) можно считать обоснованным, но необходимо иметь в виду, что при его выводе использовано конкретное выражение для векторного потенциала. Для другого выражения, например, получаемого из выражения (9) предыдущего раздела с использованием кулоновской калибровки, вид уравнения (1) изменяется, но результат (2) сохраняет силу.