Распределение векторного потенциала магнитного поля кругового кольца с током.
Считая зависимость (9) известной, а принцип суперпозиции справедливым, получаем
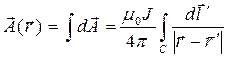 . (12)
. (12)
После вычисления соотношения (12) как векторного поля вектор магнитной индукции определяют простым дифференцированием
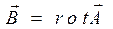 . (13)
. (13)
Векторный потенциал магнитного поля кругового кольца радиуса а с током 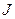 , расположенного в плоскости z=0 c центром в начале координат, в точке пространства с декартовыми координатами (x.y,z) определяется выражениями:
, расположенного в плоскости z=0 c центром в начале координат, в точке пространства с декартовыми координатами (x.y,z) определяется выражениями:
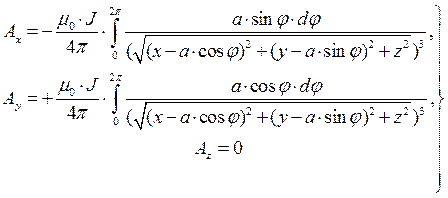 (14)
(14)
Вычисление полученных квадратур как функций произвольной точки пространства достаточно сложно. Аналитические результаты с помощью пакета символьных вычислений Maple могут быть получены при непосредственном учете осевой симметрии системы токов (при этом можно положить значение координаты y равным нулю):
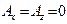 , (15)
, (15) 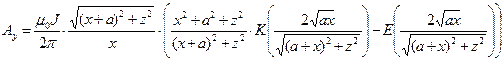 . (16)
. (16)
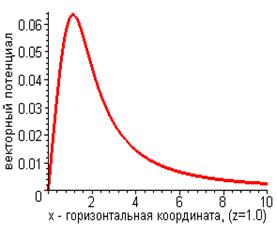
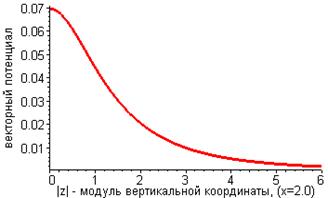
Здесь символами К и Е обозначены специальные функции математической физики – эллиптические интегралы первого и второго рода. На рис. 2 приведены результаты расчёта распределения величин проекций векторного потенциала магнитного поля, образованного круговым контуром с током.
|
|
В практических расчетах использование описанного приёма оправдано только при условии построения замкнутого аналитического выражения для компонент векторного потенциала, в противном случае использование векторного потенциала существенных преимуществ не доставляет.
Дата добавления: 2017-09-01; просмотров: 2161;

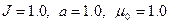 в системе СИ.
в системе СИ.










