Вывод уравнения Пуассона в электростатике.

Уравнение Пуассона для потенциала электростатического поля.

Выше мы познакомились со свойствами электростатического поля: поток вектора напряженности электростатического поля через замкнутую поверхность связан с величиной электрического заряда внутри этой поверхности (теорема Гаусса), а циркуляция вектора напряженности электростатического поля по произвольному неподвижному замкнутому контуру равна нулю (свойство потенциальности). Локальные проявления описанных свойств напряженности электростатического поля выражаются связью дивергенции вектора напряженности 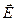с величиной объёмной плотности электрического заряда

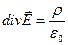(1)

и связью напряженности 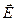с потенциалом электростатического поля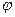 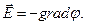(2)

Если второе из рассматриваемых соотношений подставить в первое, можно получить уравнение Пуассона, связывающее потенциал электростатического поля с величиной объёмной плотности электрического заряда:

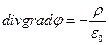. (3)

Левую часть уравнения Пуассона обычно записывают с помощью специального оператора «лапласиана скалярной функции»

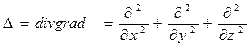. (4)

Если ввести в рассмотрение оператор Гамильтона (другое его название – «оператор набла»)

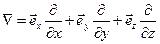, (5)

где 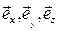- орты декартовой системы координат, то формально дивергенцию вектора 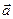можно рассматривать как результат скалярного произведения «вектора» набла на вектор 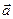, а градиент скалярной функции как произведение «вектора» набла на скаляр, только при этом надо помнить, что оператор набла – дифференциальный оператор - при записи операции должен стоять перед функцией, на которую он действует:

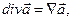
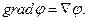(6)

Лапласиан, таким образом, можно рассматривать как последовательное применение оператора Гамильтона (оператора набла):

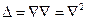. (7)

Итак, уравнение Пуассона для потенциала электростатического поля в вакууме имеет вид:

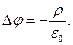(8)

В частном случае, когда объёмная плотность электрического заряда равна нулю, т.е. в рассматриваемой области отсутствуют распределенные по объёму электрические заряды, уравнение Пуассона переходит в уравнение Лапласа

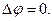(9)

Уравнение Лапласа в электростатике описывает изменение потенциала в пространстве, свободном от электрических зарядов. Значение уравнений Пуассона и Лапласа для изучения электростатических явлений чрезвычайно велико: в отличие от дифференциальной формы теоремы Гаусса эти уравнения - уравнения для единственной неизвестной функции, решение этих уравнений можно получить при самых общих предположениях о характере распределения в пространстве неподвижных и неизменных по величине электрических зарядов. Конкретные результаты получаются с обязательным учетом «граничных условий», т.е. условий, налагаемых на общее решение уравнения Пуассона спецификой рассматриваемой области пространства, свойств замыкающей область поверхности и особенностей распределения электрических зарядов по этой поверхности.

Выражение для лапласиана скалярной функции (4) записано в декартовой системе координат. В цилиндрической системе координат ( 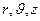) уравнение Пуассона принимает вид

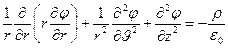, (10)

а в сферической системе координат( ) –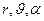

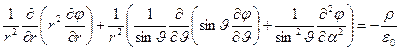. (11)

В произвольной системе координат можно воспользоваться известными определениями дивергенции вектора и градиента скалярной функции (символическая форма записи).