Следствия из уравнения Пуассона.

Уравнение Пуассона для потенциала электростатического поля является линейным дифференциальным уравнением в частных производных второго порядка. Линейность уравнения обуславливает возможность использования принципа суперпозиции для потенциала электростатического поля в вакууме, с принципом суперпозиции мы познакомились выше. Дифференциальный характер уравнения Пуассона отражает локальные свойства скалярного поля потенциала 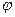. Интегральные свойства поля, естественно, связаны с локальными свойствами. Поскольку мы получили уравнение Пуассона как следствие теоремы Гаусса и условия потенциальности напряженности электростатического поля, несложно показать, что можно было бы провести рассуждения в обратном порядке и получить из уравнения Пуассона формулировку теоремы Гаусса. Это лишний раз подчёркивает глубокую связь между свойствами потенциала и напряженности электростатического поля.

В теории потенциала многие важные соотношения получают с использованием первой и второй теорем Грина (специфические следствия математической теоремы Остроградского-Гаусса) и формулы Грина. Последняя связывает между собой значение потенциала в точке наблюдения с распределением объёмной плотности заряда по контрольному объёму и распределением по контрольной поверхности потенциала и его нормальной производной. Хотя формула Грина не даёт возможности прямого вычисления искомой функции (в теории потенциала нельзя на границе области изменения независимых переменных одновременно задать значение искомой функции и значение её нормальной производной), её часто используют для нахождения формы решения и (или) сведения краевой задачи математической физики к интегральному уравнению.

2.5.4. Вариационный принцип в электростатике.

Фундаментальное значение в современной физике имеют так называемые «вариационные принципы». Первый в истории физики вариационный принцип сформулировал Герон Александрийский в III веке до н.э. Он постулировал, что луч света в системе оптических зеркал из исходной точки в конечную точку проходит по наикратчайшему пути. В элементарном курсе физики известно утверждение, что в состоянии равновесия механическая система имеет наименьшую потенциальную энергию. В электростатике тоже имеет место нечто подобное. Оказывается, что выражение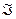

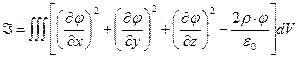,(1)

вычисленное по бесконечному пространству при произвольном распределении 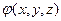и известном распределении 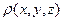(характер поведения обеих функций на бесконечности должен обеспечивать условия существования интеграла), для реального электростатического поля имеет минимальное значение. Заметим, что для каждой функции 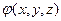величина 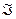принимает некоторое конкретное значение. Говорят, что 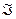является вариационным функционалом, определенным на множестве функций 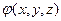. В вариационном исчислении (раздел математической теории) доказывают, что минимум функционала 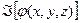достигается, если 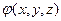удовлетворяет уравнению Пуассона. Эквивалентная форма записи вариационного функционала имеет вид:

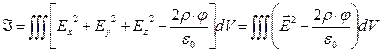.(2)

В этой форме неявно содержится понятие «объёмная плотность энергии электростатического поля», о которой мы поговорим ниже.