Потенциал электростатического поля, образованного системой электрических зарядов, расположенных известным способом в области конечных размеров.

Выражение для потенциала электростатического поля в вакууме для безграничного пространства, полученное по принципу суперпозиции элементарных электрических зарядов, должно удовлетворять уравнению Пуассона (8) раздела 2.5.1 в безграничном пространстве.

Допустим, что в некоторой области пространства имеется конечная совокупность сосредоточенных электрических зарядов, в объёме V отлична от нуля объёмная плотность, на поверхности S отлична от нуля поверхностная плотность, а вдоль контура L отлична от нуля погонная плотность электрического заряда. Выше с использованием принципа суперпозиции было получено выражение для потенциала электростатического поля для рассматриваемого случая:

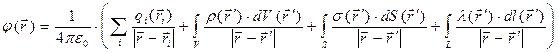. (1)

Поскольку потенциал электростатического поля должен удовлетворять уравнению Пуассона в области, где отлична от нуля объёмная плотность электрического заряда, или уравнению Лапласа в области, где отсутствует объёмная плотность электрического заряда, то, по-видимому, приведённое выражение является решением уравнения Пуассона или уравнения Лапласа в соответствующих областях пространства. Это действительно верно.

Введём в рассмотрение функцию

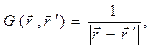(2)

её называют функцией влияния, функцией источника или функцией Грина для уравнения Лапласа в безграничном пространстве. Она обладает следующим свойством:

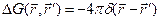, (3)

где 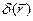- трёхмерная функция Дирака, основное функциональное свойство которой

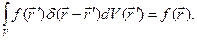(4)

Перепишем приведённое выше выражение для потенциала электростатического поля в форме:

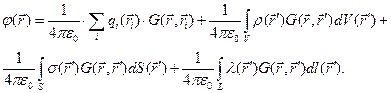(5)

Заметим, что лапласиан скалярной функции как дифференциальный оператор действует только на зависимость этой функции от координат точки наблюдения, описываемой радиусом-вектором 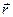. Координаты точек, описываемых радиусами-векторами 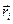в случае дискретных электрических зарядов или 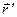в случае непрерывного распределения электрических зарядов,рассматриваются как параметры, т.е. считаются «постоянными» величинами. В частном случае 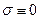имеет место результат:

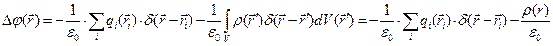. (6)

Первый член правой части полученного результата представляет собой формальное выражение для объёмной плотности сосредоточенного электрического заряда:

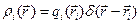. (7)

Формально распределенная по объёму величина сосредоточенного электрического заряда удобна при теоретическом анализе и решении практических задач электростатики.

Итак, мы убедились, выражение для потенциала электростатического поля в вакууме для безграничного пространства, полученное по принципу суперпозиции элементарных электрических зарядов (1), удовлетворяет уравнению Пуассона (8) раздела 2.5.1 в безграничном пространстве.

Уравнения Лапласа и Пуассона в ограниченной области пространства требуют конкретизации так называемых граничных условий, в зависимости от типа этих условий говорят о граничных (или краевых) задачах для этих уравнений. Краевая задача первого рода (задача Дирихле) возникает, если на замкнутой границе области известно распределение потенциала. Краевая задача второго рода (задача Неймана) возникает, если на замкнутой границе области известно распределение нормальной производной потенциала. Краевая задача третьего рода (смешанная краевая задача) возникает, если известна функциональная связь значений потенциала и его нормальной производной для каждой точки граничной поверхности. Теория краевых задач изучается специальным разделом математики, он называется «уравнения математической физики». Методы решения краевых задач делятся на аналитические и численные. К первым относятся метод разделения переменных, метод интегральных преобразований, метод функций Грина, вариационные метод Ритца и метод Бубнова-Галёркина. Основу численных методов составляют разностные методы и метод конечных элементов. Специальное математическое обеспечение современных персональных компьютеров содержит, в частности, «решатели» двумерных и трёхмерных краевых задач математической физики, что в немалой степени облегчает решение прикладных задач и внедрение в инженерную практику более сложных, но зато и более полных моделей физических процессов.

В современных курсах математики доказаны теоремы существования и единственности решения краевых задач для уравнений Лапласа и Пуассона и теорема о «принципе максимума». В наши задачи не входит подробное изучение этих математических теорем, а с их содержанием полезно познакомиться: их результаты эффективно используются при решении практических задач электростатики. Для задачи Дирихле для уравнения Лапласа, например, в теореме существования утверждается, что решение задачи существует, причём степень гладкости решения зависит от гладкости заданной на границе области искомой функции. В теореме о единственности утверждается, что решение задачи Дирихле для уравнения Лапласа единственно. Это означает, что если при рассмотрении практической задачи электростатики получено решение, удовлетворяющее заданным граничным условиям, то никакого другого решения не существует. Правда, надо иметь в виду, что различные методы решения краевой задачи приводят, как правило, к разным формам записи одного и того же решения задачи. Принцип максимума в теории задачи Дирихле для уравнения Лапласа очень нагляден и прост: значение решения в произвольной точке рассматриваемой области лежит между минимальным и максимальным значениями искомой функции на границе области. Принцип максимума удобно использовать для априорных оценок решения и для контроля «правильности» получаемых результатов.