Вычисление дивергенции векторного поля.

Пусть в пространстве имеется непрерывное векторное поле 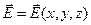. Выделим в пространстве, занятом векторным полем , элементарный объем dV в форме прямоугольного параллелепипеда со сторонами dx, dy, dz, параллельными осям декартовой системы координат с точкой M внутри.

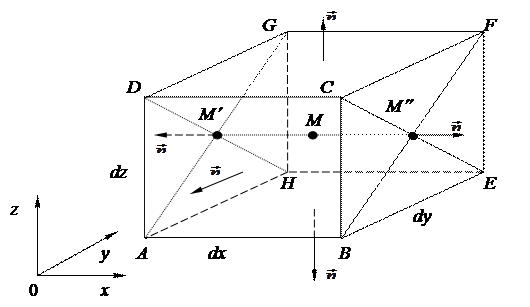
Условимся, что координаты точки M суть (x,y,z), сама точка M является точкой пересечения диагоналей параллелепипеда, точк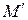и и 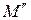– проекции точки M на левую и правую грани параллелепипеда. Рассмотрим левую грань параллелепипеда. Направление внешней нормали 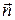для этой грани, очевидно, противоположно направлению оси x , поэтому элемент потока вектора через эту грань с точностью до членов второго порядка малости имеет вид:

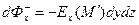. (1)

В силу непрерывности векторного поля с точностью до членов второго порядка малости имеем:

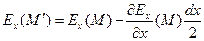, (2)

поэтому

. (3)

Для правой грани параллелепипеда направление внешней нормали совпадает с направлением оси x, элемент потока вектора через эту грань имеет вид:

. (4)

В силу непрерывности векторного поля получим:

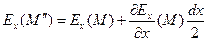, (5)

в итоге

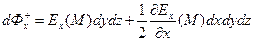. (6)

Суммарный поток вектора через рассматриваемые грани равен: 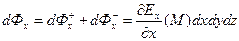. (7)

Продолжая рассуждать аналогично для оставшихся двух пар граней параллелепипеда, получим:

, (8)

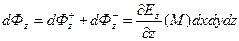. (9)

Собирая вклады в суммарный поток всех граней параллелепипеда, запишем:

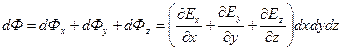. (10)

Вспоминая, что

dV=dxdydz, (11)

в соответствии с определением дивергенции векторного поля действительно получаем:

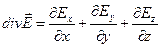(12)

в точке M с координатами (x,y,z).

В заключение заметим, что определение дивергенции векторного поля (18) предыдущего раздела инвариантно в том смысле, что позволяет вычислить дивергенцию векторного поля 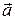в цилиндрической, сферической, вообще в произвольной системе координат, если известны выражения для элементарного объёма и площадей поверхности его граней, а для векторного поля известны его «физические» компоненты. Именно таким способом получают выражения для дивергенции векторного поля в цилиндрической системе координат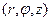

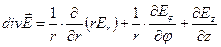(13)

и сферической системе координат : 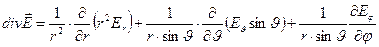. (14)

Напомним, что «физическими» компонентами вектора в криволинейной ортогональной системе координат являются его проекции на координатные направления локально введённой декартовой системы координат, орты которой совпадают по направлению с локальными ортами исходной системы.