Тензор электромагнитного поля.

Силовые характеристики электромагнитного поля – напряжённость электрического поля 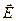и индукцию магнитного поля 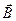- можно выразить через скалярный и векторный потенциалы электромагнитного поля в трёхмерном пространстве, а после определения 4-потенциала электромагнитного поля как 4-вектора в пространстве-времени (с мнимым временем) относительно преобразований Лоренца – как некоторую комбинацию компонент 4-потенциала. В частности,

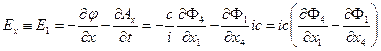, (1)

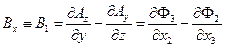. (2)

Аналогичные соотношения можно выписать и для остальных составляющих силовых характеристик электромагнитного поля. Соотношения (1) – (2) позволяют предположить, что комбинация частных производных от компонент 4-потенциала по координатам четырёхмерного пространства со специфической антисимметричной структурой

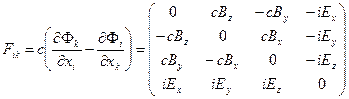(3)

является антисимметричным тензором второго ранга с ковариантными компонентами в четырёхмерном пространстве относительно преобразований Лоренца. В соответствии с этим предположением запишем правило преобразования 4-тензора 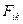при переходе из системы координат 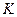в систему :

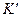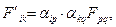
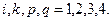(4)

В соотношении (4) матрица преобразований Лоренца 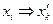( 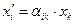) имеет вид:

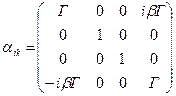(5)

Наряду с 4-тензором электромагнитного поля 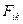в СТО рассматривают 4-тензор 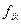, компоненты которого образованы проекциями трехмерного вектора напряжённости магнитного поля 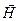и трехмерного вектора :

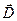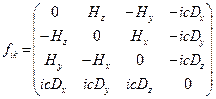(6)

и 4-тензор электрического и магнитного моментов вещества, компоненты которого образованы проекциями трёхмерного вектора поляризованности среды 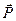и проекциями трёхмерного вектора намагниченности среды :

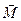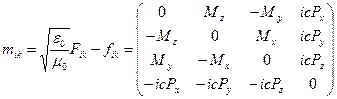. (7)

Преобразование этих величин выполняется аналогично преобразованию компонент 4-тензора электромагнитного поля.

Таким образом, могут быть получены все преобразования электромагнитных величин, рассмотренных в разделе 13.2.

13.4.2. Ковариантность системы уравнений Максвелла.

Уравнения классической электродинамики полностью описывают поведение электромагнитного поля. Они были установлены задолго до возникновения специальной теории относительности. Хотя их свойства и послужили толчком для исследований в области теории относительности, сами принципы специальной теории относительности справедливы в рамках весьма общих представлений о природе окружающего физического мира. В соответствии с принципом относительности уравнения Максвелла должны быть ковариантными относительно преобразований Лоренца. В теоретической физике понятие «ковариантность» означает идентичность формы записи основных уравнений теории при преобразованиях системы координат. Оказалось (выше это было показано с использованием непосредственных вычислений), что система уравнений Максвелла действительно сохраняет свою форму записи при переходе из системы координат 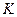в систему координат 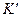с помощью преобразований Лоренца, если справедливы постулированные формулы преобразования компонент трехмерных векторов электромагнитного поля. В предыдущем разделе были введены 4-векторы электромагнитного поля. Уравнения раздела 13.3 для 4-потенциала (9) электромагнитного поля, условие калибровки Лоренца (10) и закон сохранения электрического заряда (11), эквивалентные системе уравнений Максвелла, уже имеют ковариантную форму. Но особенно наглядно это свойство системы уравнений классической электродинамики проявляется при использовании 4-тензора 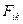электромагнитного поля, 4-тензора 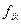составленного из компонент вспомогательных 3-векторов электромагнитного поля и вектора 4-плотности тока .

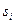Однородные уравнения Максвелла

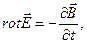
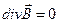(1)

можно записать в виде «одного» уравнения:

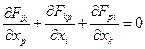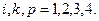, (2)

Иногда используют 4-тензор 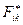, дуальный 4-тензору :

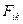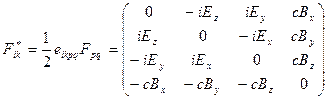. (3)

В соотношении (3) объект 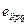- объект Леви-Чивиты - абсолютно антисимметричный объект четвертого ранга, индексы которого изменяются от 1 до 4. Составляющие этого объекта обращаются в нуль, если хотя бы значения двух индексов совпали между собой. По условию 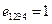, остальные составляющие этого объекта получаются из «базового» со знаком «плюс», если совокупность их индексов получается в результате чётной перестановки индексов 1,2,3,4, или со знаком «минус», если перестановка индексов нечетная (значения составляющих объекта Леви-Чивиты зависят от метрики используемой системы координат).

С помощью этого 4-тензора 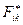однородные уравнения Максвелла записываются в форме:

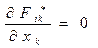. (4)

Если использовать явное выражение для 4-тензора 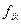- зависимость (6) предыдущего раздела, то неоднородные уравнения Максвелла принимают вид;

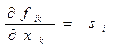. (5)

Трудно поверить, что классическая электродинамика вся целиком, со всеми приложениями укладывается в уравнения (4) и (5).

Дивергенция 4-тензора (левые части уравнений (4) и (5)) является при выбранном методе описания пространства-времени 4-вектором, значит в системе уравнений (4)-(5) установлены линейные соотношения между 4-векторами и эта форма записи является ковариантной по отношению к преобразованиям Лоренца.

В заключение раздела покажем, каким образом можно практически использовать полученные выше результаты.

Задача 1. Как преобразуется 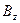- проекция трёхмерного вектора магнитной индукции на ось z при переходе из инерциальной системы отсчёта 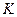в инерциальную систему отсчёта ?

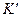Решение. Из определения 4-тензора электромагнитного поля (формула (3) предыдущего раздела) находим, что 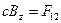. При преобразовании координат величина 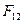переходит в 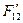. Вычислим эту величину по соотношению (4) предыдущего раздела:

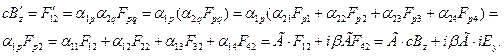(6)

Отсюда получаем

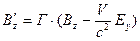. (7)

Решение получено.

Задача 2. Показать, что уравнения (4) совпадают с однородными уравнениями Максвелла.

Решение. Воспользуемся зависимостью (3) и для значений i=1,2,3,4 получим явные выражения:

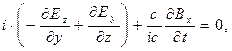
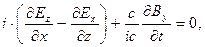
(8)

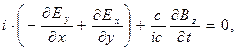
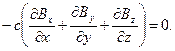
В первых трёх соотношениях угадываются проекции на декартовы оси векторного уравнения

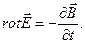(9)

Последнее соотношение записывается в символическом виде как

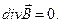(10)

Показано, что из уравнений (4) следуют однородные уравнения Максвелла в трёхмерном пространстве.

Задача 3. Показать, что уравнения (5) совпадают с неоднородными уравнениями Максвелла.

Решение. Воспользуемся зависимостями (6) предыдущего раздела для компонент 4-тензора 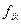и определением вектора 4-плотности тока. Последовательно для значений i=1,2,3,4 запишем явные выражения:

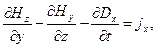
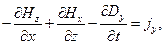(11)

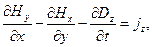
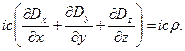
Очевидно, что первые три соотношения эквивалентны символической записи

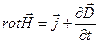, (12)

а последнее соотношение представляет собой дифференциальную форму теоремы Гаусса для вектора 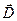. Таким образом, показано, что система уравнений (5) эквивалентна системе неоднородных уравнений Максвелла.