ПРЕДЕЛЬНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ. ЗАПАС ПРОЧНОСТИ.

Важнейшей задачей инженерного расчета является оценка прочности детали по известному напряженному состоянию. Если напряженное состояние в элементах сооружения является одноосным (линейным), то определение момента появления опасных деформаций или разрушения осуществляется достаточно просто путем сопоставления максимальных деформаций или напряжений в опасном сечении элемента конструкции с допускаемым.

Рассмотрим вопрос о прочности материала при сложном напряженном состоянии (плоском или объемном). В этом случае, как показывают опыты, для одного и того же материала опасное состояние может иметь место при различных предельных значениях главных напряжений в зависимости от соотношений между ними. Экспериментально найти величины этих предельных напряжений, как это делалось при растяжении-сжатии, не представляется возможным.

Приходится вводить некоторый критерий прочности – гипотезу (предположение) о преимущественном влиянии на прочность материала при сложном напряженном состоянии того или иного фактора, который и ответственен за возникновение опасного состояния материала.

Расчеты на прочность отдельных стержней, балок и конструкций основаны на оценке прочности материала в опасной точке.

При таких расчетах наибольшие нормальные, касательные или эквивалентные напряжения сравниваются с допускаемым напряжением. Если наибольшие расчетные напряжения не превышают допускаемых, то считается, что надлежащий запас прочности конструкции этим обеспечивается. Такой способ расчета на прочность называют расчетом по допускаемым напряжениям.

Под предельным состоянием конструкции понимают такое ее состояние, при котором она теряет способность сопротивляться внешним воздействиям.

Различают три вида предельных состояния:

- первое предельное состояние - по несущей способности (прочности, устойчивости и выносливости);

- второе предельное состояние - по развитию чрезмерных деформаций (прогибов, перекосов);

- третье предельное состояние - по образованию или раскрытию трещин.

Введение критерия прочности позволяет сопоставить данное сложное напряженное состояние с простым, (например одноосным растяжением).

Эквивалентное напряжение (σ_экв) – это напряжение, под действием которого материал в условиях простого растяжения - сжатия оказывается в равноопасном состоянии с рассматриваемым сложным напряженным состоянием.

Тогда, для того чтобы провести расчет на прочность при сложном напряженном состоянии, необходимо сначала «перейти» от сложного напряженного состояния к простому растяжению, то есть, используя наиболее подходящий для данного случая критерий прочности, найти эквивалентное напряжение. Затем необходимо сравнить это эквивалентное напряжение с допускаемым, найденным из опытов на растяжение:

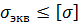
Основной задачей при выработке критерия прочности оказывается правильный выбор основного фактора, влияющего на прочность материала при сложном напряженном состоянии, и установление при этом такого эквивалентного напряжения, которое в обоих случаях дает одинаковый коэффициент запаса.

Под коэффициентом запаса в общем случае напряженного состояния принимают число, показывающее во сколько раз нужно одновременно увеличить все компоненты напряженного состояния σ₁, σ₂, σ₃, чтобы оно стало предельным.

КЛАССИЧЕСКИЕ КРИТЕРИИ ПРОЧНОСТИ (ТЕОРИИ ПРОЧНОСТИ).

- I теория прочности – теория Галилея.

Критерий наибольших нормальных напряжений

В качестве первого критерия прочности, называемого обычно первой теорией прочности, был принят критерий наибольших нормальных напряжений, в соответствии с которым причиной разрушения материала считались наибольшее (из трех главных) нормальное напряжение.

Согласно этому критерию, разрушение материала при сложном напряженном состоянии, как и при простом растяжении-сжатии, наступает от действия всего лишь одного напряжения |σ|_max, при этом действие двух других напряжений не учитывается.

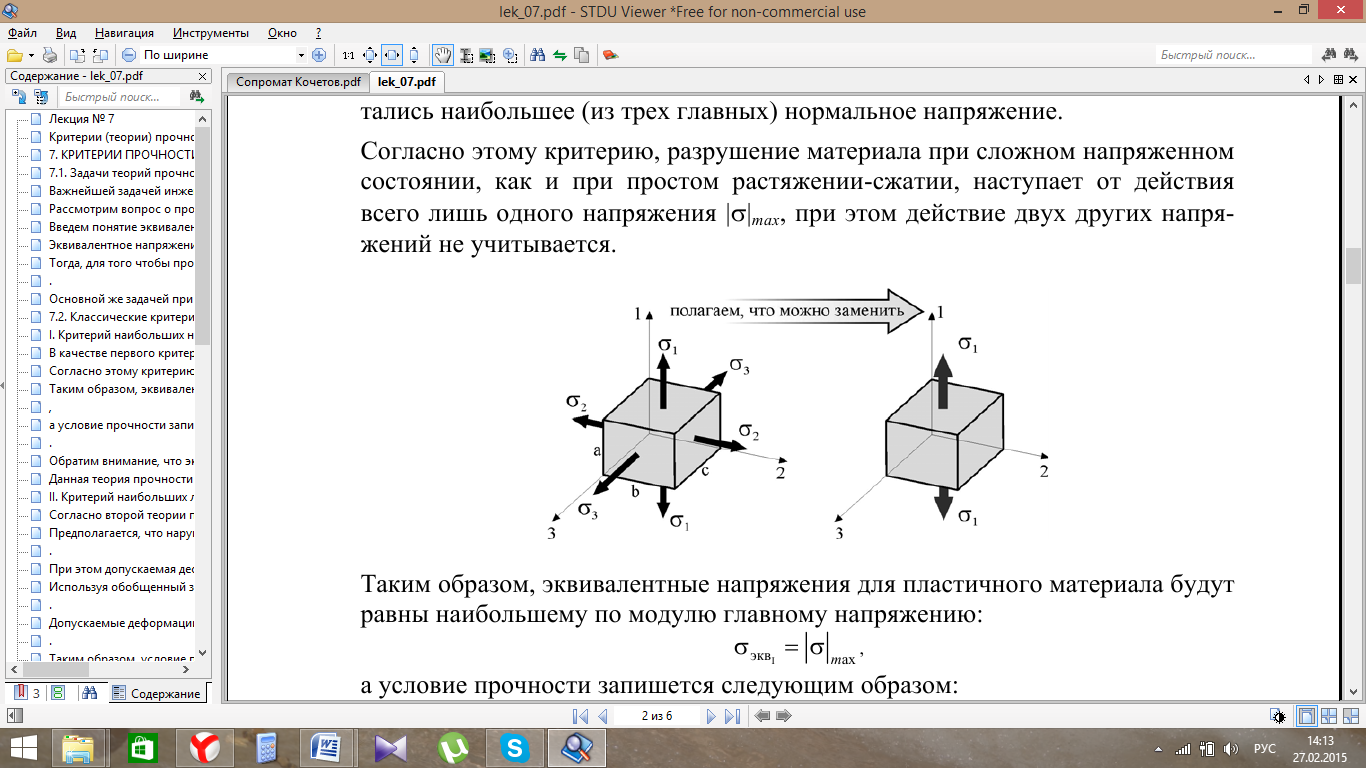
Таким образом, эквивалентные напряжения для пластичного материала будут равны наибольшему по модулю главному напряжению:

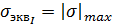
а условие прочности запишется следующим образом:

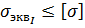
Обратим внимание, что эквивалентные напряжения всегда положительная величина.

Данная теория прочности в настоящее время практически не используется, так как она подтверждается экспериментами лишь для некоторых очень хрупких материалов (камень, кирпич, керамика и т. п.).

- II теория прочности – теория Мариотта(1662г)

Критерий наибольших линейных деформаций

Согласно второй теории прочности, в качестве критерия прочности принимают наибольшую по абсолютной величине линейную деформацию.

Предполагается, что нарушение прочности в общем случае напряженного состояния наступает тогда, когда наибольшая линейная деформация достигает своего допускаемого значения, то есть

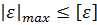
При этом допускаемая деформация материала определяется при простом растяжении-сжатии.

Используя обобщенный закон Гука, запишем данное условие прочности в напряжениях. Пусть наибольшее относительное удлинение будет равно ε₁, тогда

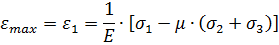
Допускаемые деформации при растяжении-сжатии связаны с допускаемыми напряжениями также по закону Гука:

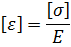
Таким образом, условие прочности можем записать в виде:

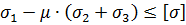
Эквивалентное напряжение в этом случае

а окончательно, условие прочности:

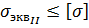
Данная теория также в настоящее время редко применяется в инженерной практике, так как находит экспериментальное подтверждение лишь для некоторых хрупких материалов (легированный чугун, высокопрочная сталь).

- III теория прочности – теория Кулона(1773г)

Критерий наибольших касательных напряжений

Здесь в качестве критерия прочности принята величина наибольшего касательного напряжения. Согласно этой теории, предполагается, что предельное состояние материала наступает, когда наибольшее касательное напряжение достигает своего допускаемого значения, которое определяется из опытов на растяжение-сжатие. В этом случае условие прочности принимает вид:

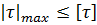
Максимальные касательные напряжения при объемном напряженном состоянии определяются как

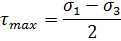
тогда допускаемые касательные напряжения, определяемые при простом растяжении, можно найти следующим образом:

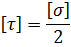
Таким образом, окончательно, условие прочности по III теории прочности запишем в виде:

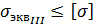
где эквивалентное напряжение

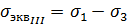
Третья теория прочности хорошо подтверждается опытами для материалов, одинаково работающих на растяжение и сжатие. Недостаток ее заключается в том, что она не учитывает среднего по величине главного напряжения σ₂, которое, как показывают эксперименты, также оказывает, хотя и не значительное, влияние на прочность материалов.

- IV теория прочности – теория Мизеса – Гемки.