Критерий удельной потенциальной энергии формоизменения
В качестве критерия прочности в этом случае принимают количество удельной потенциальной энергии формоизменения, накопленной деформированным элементом. Согласно этой теории, опасное состояние наступает тогда, когда удельная потенциальная энергия формоизменения достигает своего предельного значения, которое определяется из опытов на простое растяжение-сжатие. Здесь условие прочности можно записать так:
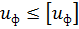

Запишем удельную потенциальную энергию формоизменения через главные напряжения при объемном напряженном состоянии
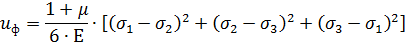
откуда при растяжении-сжатии
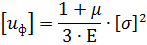
Отсюда, условие прочности, записанное через нормальные напряжения:
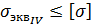
при этом эквивалентные напряжения будем определять по формуле:
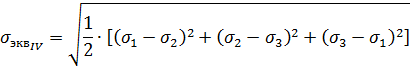
Опыты хорошо подтверждают четвертую теорию для пластичных материалов, одинаково работающих на растяжение и сжатие. При этом четвертая теория более точно, чем третья, описывает появление в материале малых пластических деформаций. По сути дела эти две теории более правильно называть теориями пластичности.
- V теория прочности. Теория Мора
Согласно теории Мора, два напряженных состояния равноопасны, если для соответствующих двух главных напряжений (σ′1, σ′3 и σ′′1, σ′′3) соблюдается соотношение
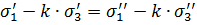
Отсюда вытекает формула для эквивалентного напряжения:
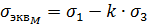
Здесь коэффициент k представляет собой отношение предельных напряжений при одноосном растяжении и при одноосном сжатии. Если принять, что коэффициенты запаса прочности по отношению к предельным напряжениям растяжения и сжатия одинаковы, то k можно определить из выражения:
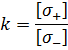
Окончательно условие прочности по теории Мора запишется следующим образом
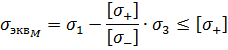
Теория прочности Мора позволяет установить сопротивление разрушению материалов, обладающих разными сопротивлениями растяжению и сжатию. Как видим, гипотеза Мора (как и III теория) не учитывает влияния промежуточного главного напряжения σ2 – это несомненный ее недостаток. Опыты показывают, что достаточно точные результаты гипотеза Мора дает для напряженных состояний смешанного типа, то есть для тех случаев, когда σ1 и σ3 имеют разные знаки.
Таким образом, для практических расчетов следует рекомендовать четвертую (или третью) теории прочности для материалов, одинаково сопротивляющихся растяжению и сжатию, и теорию Мора – для материалов, различно сопротивляющихся растяжению и сжатию, то есть для хрупких материалов (для них в настоящее время пока еще применяют и вторую теорию прочности).
Задача. Определить допускаемые значения напряжений σ1 по теориям прочности.
Дано: Допускаемые напряжения на растяжение: [σР] = 600кг/см2;
Допускаемые напряжения на сжатие: [σС] = 1800кг/см2;
Коэффициент Пуассона μ =0,25
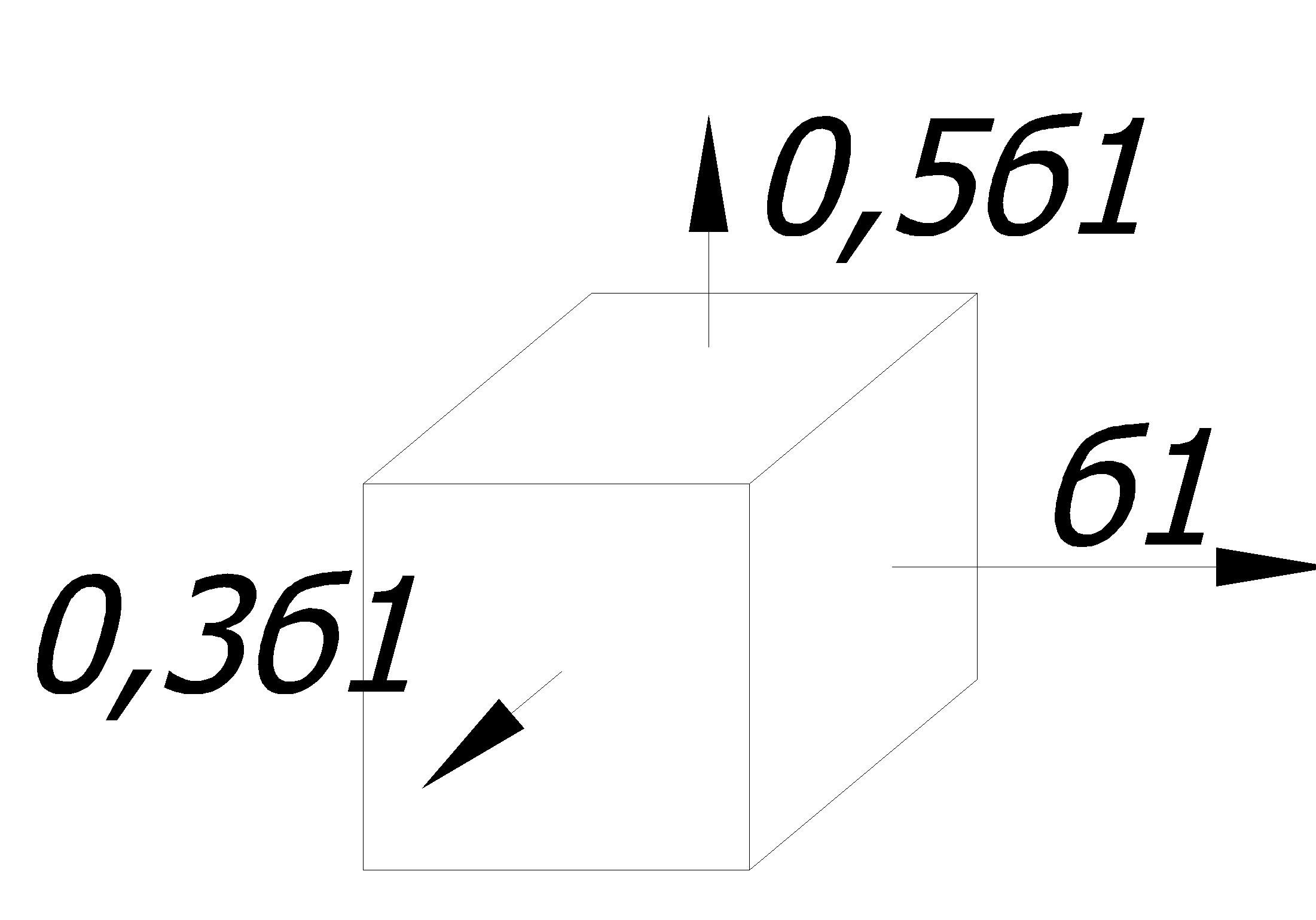
Решение:
По первой теории прочности для случая, когда все три главных напряжения являются растягивающими, получим:
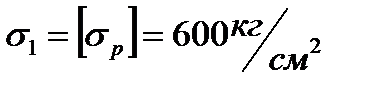
По второй теории прочности, получим:
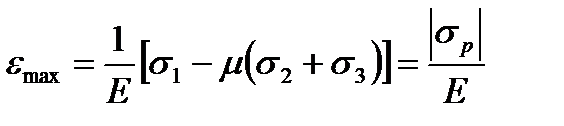


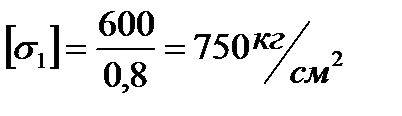
По третьей теории прочности, получим:
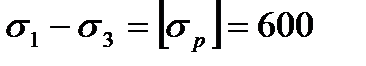
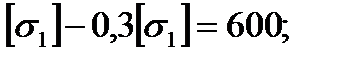
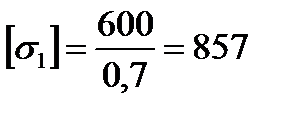
По четвертой теории прочности, получим:
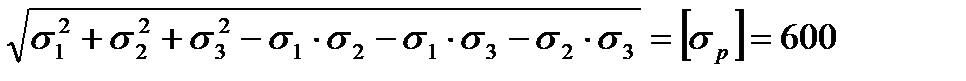
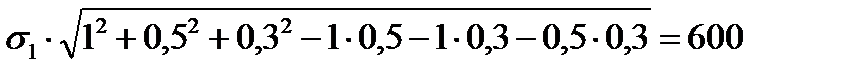
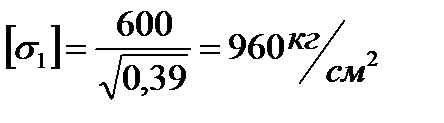
Таким образом по различным теориям прочности допускаемое значение напряжения 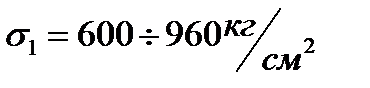
Дата добавления: 2017-06-13; просмотров: 3279;











