Свойства уравнений Максвелла

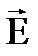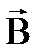Уравнения Максвелла линейны. Они содержат только первые производные полей и по времени и пространственным координатам, а так же первые степени плотности электрических зарядов ρ и токов γ. Свойство линейности уравнений непосредственно связано с принципом суперпозиции. Уравнения Максвелла содержат уравнение непрерывности, выражающее закон сохранения электрического заряда: 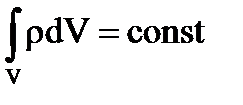Уравнения Максвелла выполняются во всех инерциальных системах отсчёта. Они являются релятивистски-инвариантными, что подтверждается опытными данными. О симметрии уравнений Максвелла. Уравнения не симметричны относительно электрического и магнитного полей. Это обусловлено тем, что в природе существуют электрические заряды, но нет магнитных зарядов. Вместе с тем в нейтральной однородной среде, где ρ = 0 и 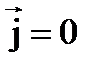,уравнения Максвелла приобретают симметричный вид, т.е. 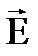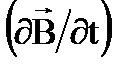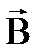так связано с , как с .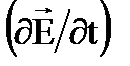

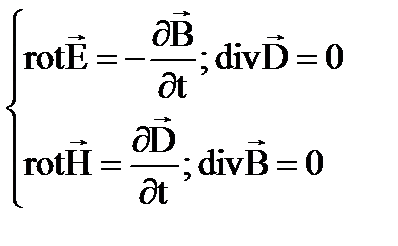
Из уравнений Максвелла следует важный вывод о существовании принципиально нового физического явления: электромагнитное поле способно существовать самостоятельно без электрических зарядов и токов. При этом изменение его состояния обязательно имеет волновой характер. Всякое изменение во времени магнитного поля возбуждает поле электрическое, изменение электрического поля, в свою очередь, возбуждает магнитное поле. За счёт непрерывного взаимопревращения они и должны сохранятся. Поля такого рода называются электромагнитными волнами. Выяснилось также, что ток смещения 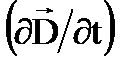играет в этом явлении первостепенную роль.