Движение частиц в магнитных и электромагнитных полях

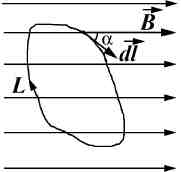
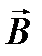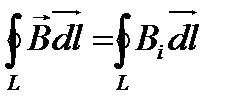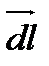Циркуляцией вектора по заданному замкнутому контуру Lназывается следующий интеграл по этому контуру: где – элемент длины контура, направленный вдоль обхода контура; B_l=Bcosα– Составляющая вектора 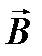в направлении касательной к контуру, с учетом выбранного направления обхода; 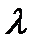– угол между векторам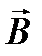и и .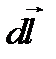

Теорема о циркуляции вектора B(закон полного магнитного поля в вакууме): циркуляция вектора 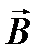по произвольному замкнутому контуру равна произведению магнитной постоянной μ₀на алгебраическую сумму токов, охватываемых этим контуром: 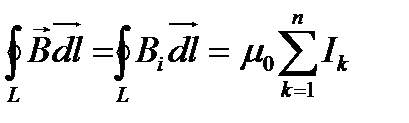, где n– число проводников с токами, охватываемых контуром произвольной формы.

Эта теорема справедлива только для поля в вакууме, поскольку для поля в веществе надо учитывать молекулярные токи. Каждый ток учитывается столько раз, сколько он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта.

Вопросы для самоконтроля:

1) Как взаимодействуют между собой параллельные токи? Чем вызывается их взаимодействие?

2) В каких единицах измеряется магнитная индукция в СИ? Сформулируйте определение этой единицы. Что называют магнитным полем? Каковы его основные свойства?

3) Перечислите правила, определяющие направление магнитного поля (линий магнитной индукции)? Поясните, как пользоваться каждым из правил.

4) Что представляет собой вектор магнитной индукции и физической интерпретации?

5) Как определяют модуль вектора магнитной индукции? Какой формулой его выражают?

6) На что Действует сила Лоренца, относительно магнитного поля?

7) В чем заключается подобие векторных характеристик электростатического и магнитного полей?

8) Контактная разность потенциалов? Явление Пельтье, Зеебека и Томсона?

9) Электронные и дырочные токи? Есть ли отличие в перемещении свободного электрона и электрона в периодическом поле решетки?

Список литературы

Основная

1.Пронин, В.П. Краткий курс физики / В. П. Пронин. – Саратов: ФГОУ ВПО «СаратовскийГАУ», 2007 г. – 200 с.

Дополнительная

1. Грабовский, Р.И. Курс физики. 6-е изд. / Р. И. Грабовский. – СПБ. : Издательство «Лань», 2002. – 608 с

Лекция 13