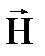Поле соленоида и тороида
Теорема о циркуляции 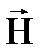 , имеет в учении о магнитном поле такое же значение, как теорема Гаусса в электростатике. В частности, подобно тому, как при симметричном распределении зарядов, теорема Гаусса позволяла вычислить
, имеет в учении о магнитном поле такое же значение, как теорема Гаусса в электростатике. В частности, подобно тому, как при симметричном распределении зарядов, теорема Гаусса позволяла вычислить 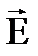 , не прибегая к закону Кулона, и имела вид (в системе СИ:N = Sqi): теорема о циркуляции
, не прибегая к закону Кулона, и имела вид (в системе СИ:N = Sqi): теорема о циркуляции 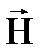 позволяет рассчитать напряженность магнитного поля при наличии симметрии токов без применения закона Био-Савара-Лапласа, что облегчает вычисления. Циркуляцией магнитного поля по заданному контуру L называется интеграл вида:
позволяет рассчитать напряженность магнитного поля при наличии симметрии токов без применения закона Био-Савара-Лапласа, что облегчает вычисления. Циркуляцией магнитного поля по заданному контуру L называется интеграл вида: 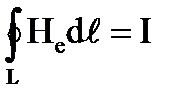
Если контур охватывает несколько токов, то:
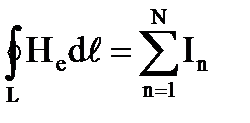
Теорема о циркуляции (закон полного тока): циркуляция вектора напряженности магнитного поля по замкнутому контуру численно равна алгебраической сумме токов, охватываемых этим контуром.
Пример №1
| 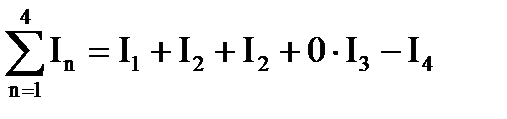
|
Пример №2
Расчёт напряженности магнитного поля внутри соленоида:
| Линии напряженности расположены внутри соленоида и практически равны нулю вне его при условии ℓ >>D. Возьмем контур 12341, тогда:
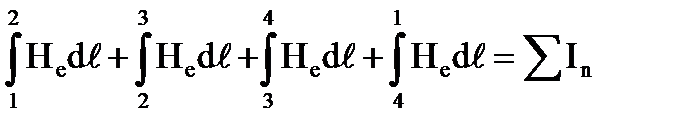
|
SIn = In, где
n– число витков, охватываемых контуром.
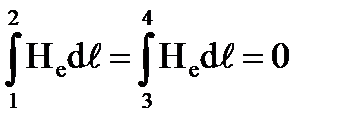 ,т.к. лучи контура ^ к линиям поля (Hе = 0);
,т.к. лучи контура ^ к линиям поля (Hе = 0);
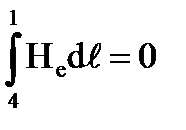 т.к. H вне контура (H = 0)
т.к. H вне контура (H = 0)
Значит: 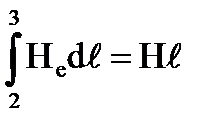 , тогда Hℓ = In
, тогда Hℓ = In
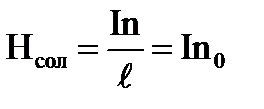 , где
, где 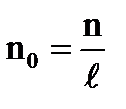 –число витков на единицу длины.
–число витков на единицу длины.
Пример №3
|
| Напряженность поля внутри тороида.
Нтор = In0; справедлива при ℓ >>D.
ℓ – средняя линия тороида (линии по оси витков).
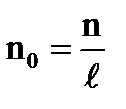
|
Дата добавления: 2017-06-13; просмотров: 1530;