Заряды. Функции с ограниченным изменением.
Пусть задано измеримое пространство (X, S). Отображение n : S®R называется зарядом (или знакопеременной мерой), если n(f) = 0 и функция n счётно-аддитивна, т. е. из разложения 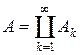 ,
, 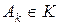 ,
, 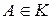 , следует, что
, следует, что 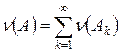 .
.
Мы рассматриваем заряды, принимающие лишь конечные значения.
Пример 1. Пусть 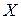 – пространство с мерой m, S – s-кольцо измеримых подмножеств из X,
– пространство с мерой m, S – s-кольцо измеримых подмножеств из X, 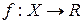 – функция, интегрируемая на X. Тогда функция множества
– функция, интегрируемая на X. Тогда функция множества
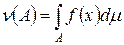 (1)
(1)
является зарядом.
Пример 2. Пусть на X заданы две меры m1 и m2 их разность, 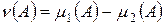 очевидно, является зарядом.
очевидно, является зарядом.
Пусть 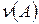 – заряд, заданный по формуле (1). Обозначим
– заряд, заданный по формуле (1). Обозначим 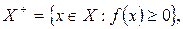
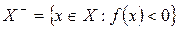 . Получаем представление
. Получаем представление
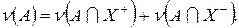 (2)
(2)
Так как на множестве 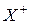 функция f положительна, то
функция f положительна, то 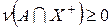 и, значит,
и, значит, 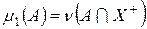 – мера. Аналогично
– мера. Аналогично 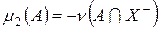 является мерой. Получаем представление заряда
является мерой. Получаем представление заряда 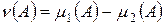 в виде разности двух мер.
в виде разности двух мер.
Измеримое множество 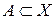 называется положительным (отрицательным) относительно заряда n, если для любого измеримого подмножества
называется положительным (отрицательным) относительно заряда n, если для любого измеримого подмножества 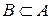 ,
, 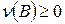
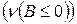 . Пустое множество является и положительным и отрицательным. Положительные (отрицательные) множества образуют s– алгебру.
. Пустое множество является и положительным и отрицательным. Положительные (отрицательные) множества образуют s– алгебру.
Теорема 1. Для любого заряда n, заданного на s-алгебре 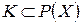 существуют такие непересекающиеся множества
существуют такие непересекающиеся множества 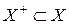 и
и 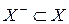 , что
, что 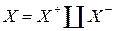 , где
, где 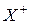 – положительное,
– положительное, 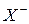 – отрицательное множества.
– отрицательное множества.
Следствие. Для любого заряда n существуют меры m1 и m2, обладающие свойством 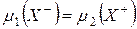 , называемым сингулярностью, что
, называемым сингулярностью, что 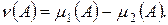
Рассмотрим подробнее заряды на s-алгебре, порожденной полуинтервалами на отрезке 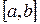 . Каждому заряду n (как и мере) поставим в соответствие функцию g. Опишем класс функций на
. Каждому заряду n (как и мере) поставим в соответствие функцию g. Опишем класс функций на 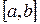 , которые соответствуют зарядам. Построение заряда аналогично построению меры Лебега-Стилтьеса по неубывающей функции.
, которые соответствуют зарядам. Построение заряда аналогично построению меры Лебега-Стилтьеса по неубывающей функции.
Функция 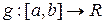 называется функцией ограниченной вариации (ограниченного изменения), если существует
называется функцией ограниченной вариации (ограниченного изменения), если существует 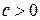 , что для любого разбиения отрезка
, что для любого разбиения отрезка 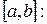
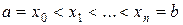 справедливо неравенство
справедливо неравенство
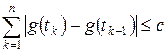
Наименьшая из констант c, при которых справедливо неравенство, называется вариацией функции g на 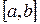 и обозначается
и обозначается 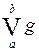 . По определению
. По определению
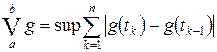 ,
,
где верхняя грань берется по множеству разбиений.
Дата добавления: 2021-07-22; просмотров: 577;











