Примеры решения задач. Доказать, что произвольная функция f (x) интегрируема

Задача 1. Пусть функция F(x) порождает меру Лебега-Стилтьеса на [ –2, 2 [. Доказать, что произвольная функция f (x) интегрируема на [–2, 2 [ относительно меры 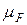и

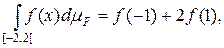если F(x)=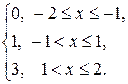

Решение. Отметим, что все подмножества интервала [-2,2[ измеримы и поэтому каждая функция f(x), x Î [-2,2[ измерима относительно меры 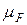. Представим полуинтервал [-2,2[ в виде объединения непересекающихся множеств [ –2, 2[ = [–2, –1[ Ç {–1} Ç ]–1,1[ Ç {1} Ç ]1,2[.

Множества [-2,1[, ]-1,1[, ]1,2[ имеют меру нуль, так как функция, порождающая меру 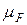, на этих множествах постоянна, а тогда каждая функция f (x) интегрируема и интеграл от неё равен нулю.

На множествах {-1} и {1} функция постоянна, а значит, простая. Поэтому

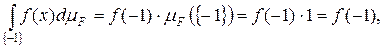
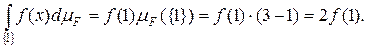
Следовательно, произвольная функция f (x) интегрируема на [-2,2[ и интеграл равен 2f (1)+f (–1). Данная функция будет интегрируема на всей числовой прямой, если

F(x)= 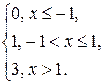тогда

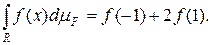
Задача 2. Вычислить интеграл Римана-Стилтьеса

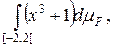где F(x)=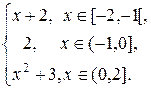

Решение. Если функция f (x) непрерывна на [a, b], а функция F (x) имеет на [a, b] всюду, кроме конечного числа точек 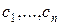интегрируемую по Риману производную 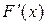, то существует интеграл Римана-Стилтьеса и

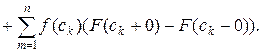
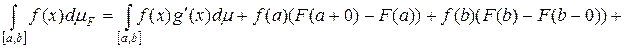
Тогда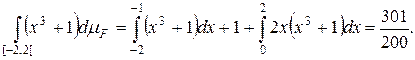

Задача 3. Пусть X=[0,1[, S={[a,b[ÌX}, h(x) – некоторая неотрицательная интегрируемая по Риману на отрезке [0,1] функция; 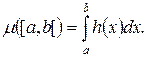Вычислить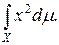

Решение. Построим последовательность простых интегрируемых функций, равномерно сходящуюся к 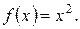Представим 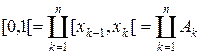так, что 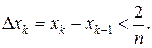По теореме о среднем для интеграла Римана 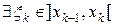такая, что 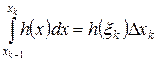, т.е. .

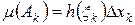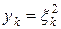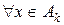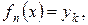
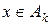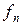Положим для , тогда и равномерно сходится к 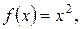т.к. при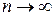

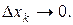
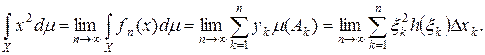
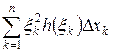есть интегральная сумма Римана, построенная для непрерывной функции 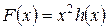на отрезке [0,1]. Так как при 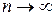, , 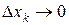то

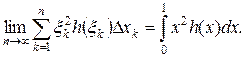Итак,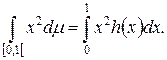

Задача 4. Пусть на [0,3[ задана мера Лебега–Стилтьеса, порожденная функцией

F(x) =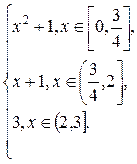

Проверить, что F не убывает и непрерывна слева. Найти:

1) меру одноточечного множества;

2) промежутки, на которых эта мера совпадает с мерой Лебега;

3) промежутки,имеющие нулевую меру;

4) промежутки, на которых эта мера абсолютно непрерывна относительно меры Лебега;

5) найти меру канторова множества K и меру множества рациональных чисел на [0,3[.

Для функции

f (x) =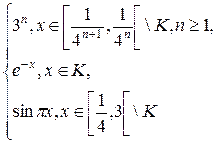

вычислить интеграл по мере Лебега – Стилтьеса, порожденной функций F, если он существует.

Решение. Функция F(x) кусочно непрерывна, имеет одну точку разрыва x = 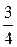, причем 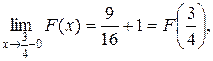что означает непрерывность слева функции F. Остановимся на пунктах 1) – 5).

1) Известно, что для любого xÎ[0,3[ 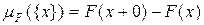. В нашем случае

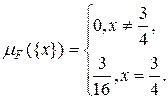
2) На промежутке 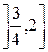мера Лебега-Стилтьеса совпадает с мерой Лебега.

3) 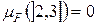, так как F постоянна.

4) Покажем, что на 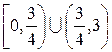мера Лебега-Стилтьеса 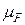абсолютно непрерывна относительно меры Лебега 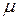. Достаточно рассмотреть промежуток 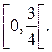Поскольку

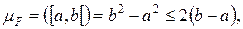то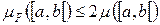

и, следовательно, 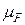– абсолютно непрерывна.

Таким образом, полуинтервал [0,3[ разбивается на четыре части:

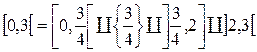и на каждой части мера 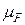описана выше.

5) Рассмотрим канторово множество K:

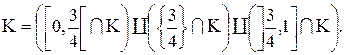
Так как 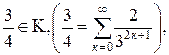то 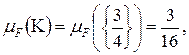потому что на промежутках абсолютной непрерывности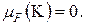

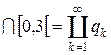Q и .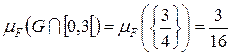

Для вычисления интеграла построим эквивалентную функцию g(x), которая отличается от f(x) только в точках множества 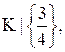мера которого равна нулю. Пусть

g(x) =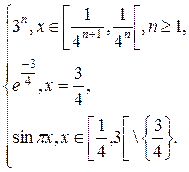

Тогда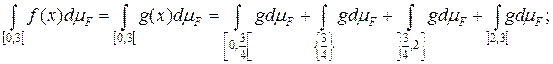

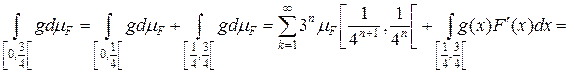
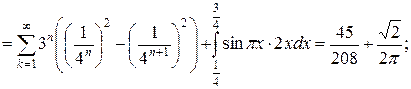
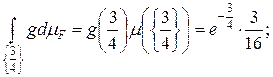
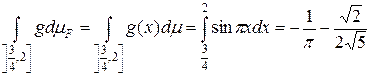
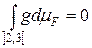
Итак,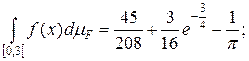

Задача 5. Определить полную вариацию функций F на указанном отрезке, если:

1) F(x) =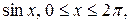

2) F(x) =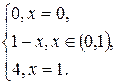

Решение. 1) Функция F является монотонной на отрезках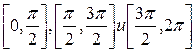

Поэтому функция 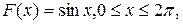имеет ограниченное изменение и

.

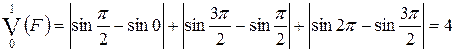2) Рассмотрим произвольное разбиение П отрезка 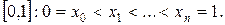Для этого разбиения

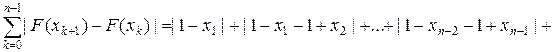
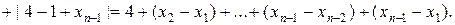
Отсюда следует, что

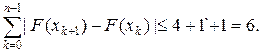
Кроме того, рассмотрим разбиение 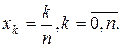В этом случае, 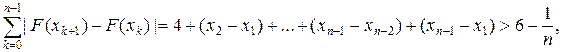поэтому sup 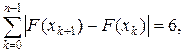т.е. .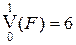

Задача 6. Доказать, что функция F(x) = 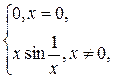не имеет ограниченного изменения на отрезке .

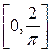Решение. Отметим, что функция F имеет неограниченную производную.

Рассмотрим для произвольного натурального числа n разбиение 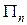отрезка 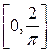точками, в которых функция 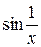равна поочередно –1 и 1, т.е.

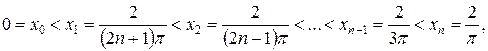и вычислим сумму 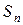модулей приращений функций F на отрезках разбиения

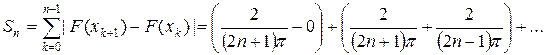
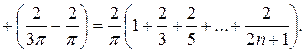
Поскольку ряд 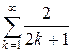расходящийся, то последовательность его частичных сумм не ограничена сверху, т.е. 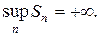Следовательно, функция F не имеет ограниченного изменения.

Задание 1. Пусть на [a,b[ задана мера Лебега-Стилтьеса, порожденная функцией g. Проверить, что g не убывает и непрерывна слева. Найти:

1) меру каждого одноточечного множества;

2) промежутки, на которых эта мера совпадает с мерой Лебега;

3) промежутки, имеющие нулевую меру;

4) промежутки, на которых эта мера абсолютно непрерывна относительно меры Лебега;

5) найти меру канторова множества K и множества рациональных чисел Q.

Для функции f вычислить интеграл по мере Лебега-Стилтьеса, если он

существует, используя следующую формулу:

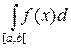m_g = +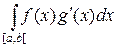

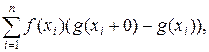
где x₁, x₂,…, x_n – точки разрыва функции g.

1.1. f (x) = 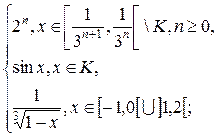g(x) =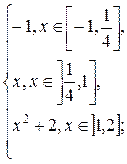

1.2. f (x) = 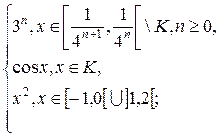g(x) =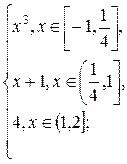

1.3. f (x) = 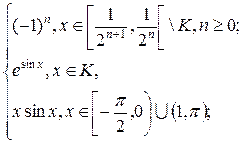g(x) =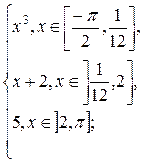

1.4. f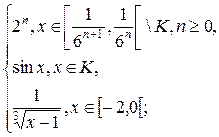(x) = g(x)=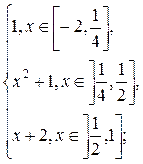

1.5. f(x) = 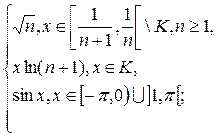g(x) =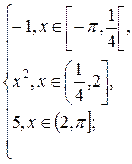

1.6. f(x) = 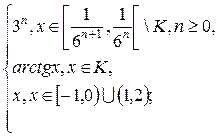g(x) =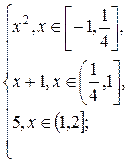

1.7. f(x) = 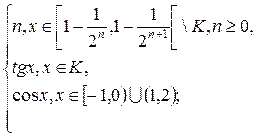g(x) =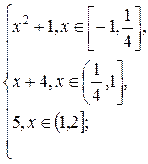

1.8. f(x) = 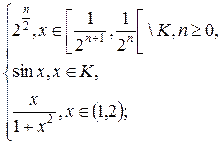g(x) =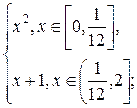

1.9. f(x) = 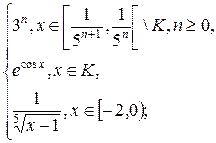g(x) =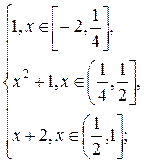

1.10. f(x) = 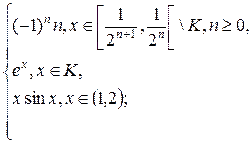g(x) =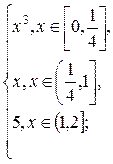

1.11. f(x) = 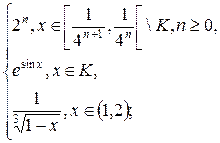g(x) =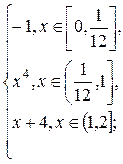

1.12. f(x) = 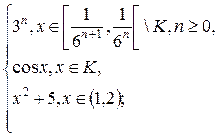g(x) =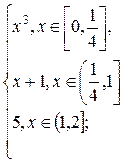

1.13. f(x) = 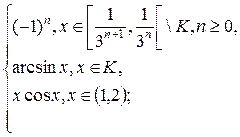g(x) =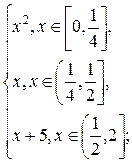

1.14. f(x) = 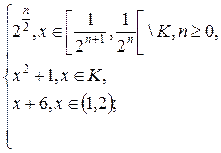g(x) =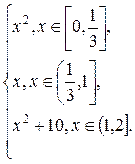

Задание 2. Вычислить интеграл Римана-Стилтьеса.

2.1. 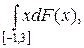F(x) =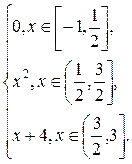

2.2. 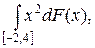F(x) =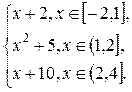

2.3. 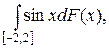F(x) =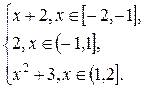

2.4. 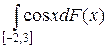, F(x) =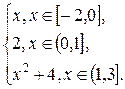

2.5. 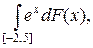F(x) =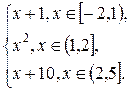

2.6. 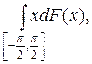F(x) = | sin x |.

2.7. 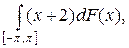F(x) =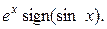

2.8. 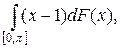F(x) = cos x × sign x.

2.9. 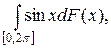F(x) =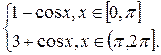

2.10. 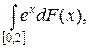F(x) = sin x × sign x.

2.11. 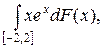F(x) =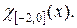

2.12. 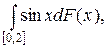F(x) =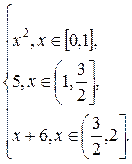

2.13. 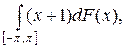F(x) = x × sign(cos x).

2.14. 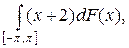F(x) = sin x × sign(cos x).

Задание 3. Выяснить, ограничена ли вариация у следующих функций. При положительном ответе вычислить вариацию функций f.

3.1. F(x) =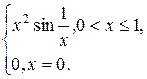

3.2. F(x) =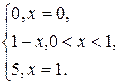

3.3. F(x) =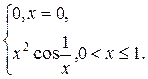

3.4. F(x) =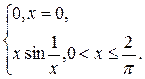

3.5. F(x) =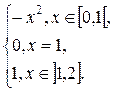

3.6. F(x) =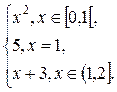

3.8. F(x) =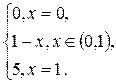

3.9. F(x) =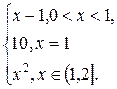

3.10. F(x) =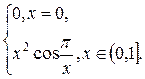

3.11. F(x) =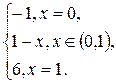

3.12. F(x) =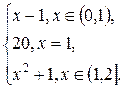

3.13. F(x) =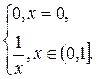

3.14. F(x) =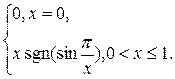

3.15. F(0) = 0; F 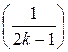= 0; F 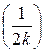= 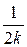и линейна на каждом отрезке.