Интеграл Лебега-Стилтьеса. Связь с интегралом Римана-Стилтьеса

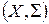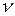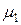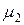Пусть задано измеримое пространство и заряд . Поскольку заряд можно представить в виде разности двух конечных мер и , то функция интегрируемая по каждой из мер будет интегрируема по заряду. Этот интеграл обладает всеми свойствами обычного интеграла Лебега.

Рассмотрим пример интеграла по заряду.

Пусть на отрезке 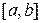задана неубывающая непрерывная слева функция g. Тогда эта функция на s-алгебре множеств 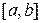определяет конечную меру Лебега-Стилтьеса. Интеграл Лебега, построенный по этой мере, называют интегралом Лебега-Стилтьеса и обозначают

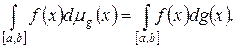
Рассмотрим частные случаи:

1. Функция g – функция скачков (т.е. 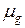– дискретная мера), тогда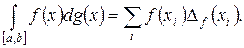

2. Функция g – абсолютно непрерывна, тогда

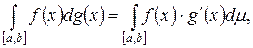
т.е. обычный интеграл Лебега.

3. Функция g, непрерывная слева на [a,b], функция с ограниченным изменением. Тогда ее можно представить в виде разности двух неубывающих функций 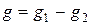непрерывных слева. Поэтому

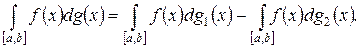
Ясно, что это интеграл Лебега по заряду 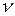, построенному по функции с ограниченным изменением. В общем случае он не сводится к интегралу Лебега.

Помимо интеграла Лебега-Стилтьеса на прямой можно определить интеграл Римана-Стилтьеса. Он вводится как предел интегральных сумм, аналогичных обычным интегральным суммам Римана. Пусть f – произвольная функция на [a,b], g – непрерывная слева функция с ограниченным изменением.

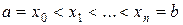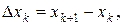
Рассмотрим некоторое разбиение отрезка [a,b]: , 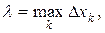выберем 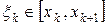и составим интегральную сумму

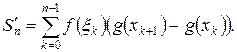
Если эти интегральные суммы при 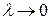имеют конечный предел, не зависящий от способа разбиения отрезка и от выбора точек 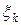, то этот предел называют интегралом Римана-Стилтьеса от функции f по функции g.

Теорема 3. Если функция f непрерывна на [a,b], то ее интеграл Римана-Стилтьеса существует и совпадает с соответствующим интегралом Лебега-Стилтьеса.