Сравнение интеграла Лебега с интегралом Римана
Для простоты рассмотрим эту связь в одномерном случае.
Теорема 1.Если для функции, заданной на [a,b], существует собственный интеграл Римана 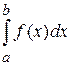 , то она интегрируема и по Лебегу и её интеграл Лебега
, то она интегрируема и по Лебегу и её интеграл Лебега 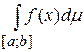 равен интегралу Римана.
равен интегралу Римана.
Теорема 2.Для того, чтобы ограниченная на отрезке [a,b] функция, была интегрируема по Риману на этом отрезке, необходимо и достаточно, чтобы множестве её точек разрыва имело меру нуль.
Из этой теоремы, в частности, следует теорема об интегрируемости по Риману монотонной функции (так как множество точек разрыва монотонной функции не более чем счётно).
Пусть функция f неограничена на полуинтервале [a,b[ и интегрируема по Риману на любом промежутке [a,b-e]. В этом случае речь идёт о несобственном интеграле Римана
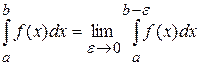 ,
,
если предел существует и конечен. Несобственный интеграл Римана называют абсолютно сходящимся, если сходится интеграл 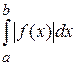 .
.
Теорема 3.Для абсолютной сходимости несобственного интеграла 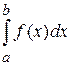 необходимо и достаточно, чтобы f была интегрируемой по Лебегу на [a,b]. При выполнении любого из этих условий имеет место равенство
необходимо и достаточно, чтобы f была интегрируемой по Лебегу на [a,b]. При выполнении любого из этих условий имеет место равенство 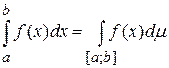 .
.
Рассмотрим интегрирование по множеству бесконечной меры. Пусть функция определена на промежутке [a,+¥[ и интегрируема по Риману на любом отрезке [a,b]. Тогда несобственный интеграл Римана по промежутку [a,+¥[ определяется как предел
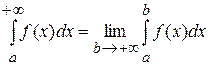 .
.
Если предел конечен, то несобственный интеграл называют сходящимся; его называют абсолютно сходящимся, если сходится интеграл 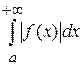 .
.
Теорема 4.Для абсолютной сходимости несобственного интеграла Римана необходимо и достаточно, чтобы функция f была интегрируема по Лебегу на [a,+¥[. При выполнении любого из этих условий имеет место равенство 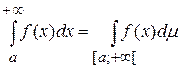 .
.
Примеры решения задач
Задача 1. Выяснить, интегрируемы ли по Лебегу на отрезке [0; 1] следующие функции:
1) 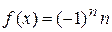 , если
, если 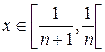 ,
, 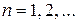 ;
;
2) 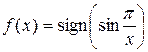 ,
, 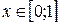 .
.
Решение.1) Функция 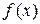 является неограниченной, поэтому по Риману она не интегрируема. f измерима, так как принимает счётное число значений на измеримых множествах
является неограниченной, поэтому по Риману она не интегрируема. f измерима, так как принимает счётное число значений на измеримых множествах 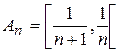 , и является простой. Для интегрируемости функции f необходимо, чтобы ряд
, и является простой. Для интегрируемости функции f необходимо, чтобы ряд
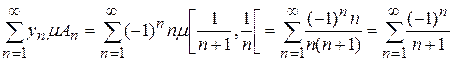
сходился абсолютно. Но ряд 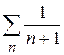 расходится, поэтому f не интегрируема по Лебегу.
расходится, поэтому f не интегрируема по Лебегу.
2) Рассматриваемая функция 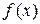 также является простой, принимающей три значения: 1, -1 и 0. А именно:
также является простой, принимающей три значения: 1, -1 и 0. А именно: 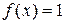 на множестве
на множестве 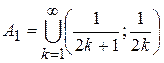 ,
, 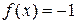 на
на 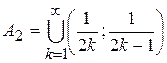 и
и 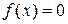 на
на 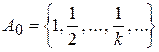 . Множества
. Множества 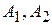 открыты, а поэтому измеримы. Кроме того
открыты, а поэтому измеримы. Кроме того
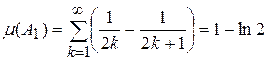 ,
,
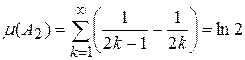 .
.
Счётное множество 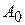 также измеримо и
также измеримо и 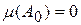 . Поэтому
. Поэтому
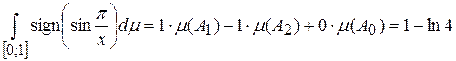 .
.
Задача 2. Интегрируема ли по Риману, по Лебегу функция 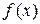 , если да, то вычислить интеграл.
, если да, то вычислить интеграл.
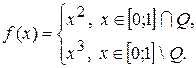
Решение.Функция 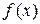 не интегрируема по Риману, так как она разрывна в каждой точке, за исключением точек
не интегрируема по Риману, так как она разрывна в каждой точке, за исключением точек 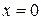 ,
, 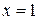 , то есть мера её точек разрыва не меньше 1. Действительно, для
, то есть мера её точек разрыва не меньше 1. Действительно, для 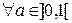
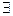
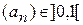 ÈQ и
ÈQ и 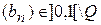 такие, что
такие, что 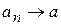 и
и 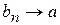 , но
, но 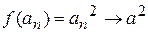 , а
, а 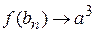 , при этом
, при этом 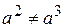 , то есть интервал ]0,1[ – подмножество множества точек разрыва функции.
, то есть интервал ]0,1[ – подмножество множества точек разрыва функции.
Выясним, интегрируема ли функция по Лебегу. Так как эквивалентные функции интегрируемы или неинтегрируемы одновременно и их интегралы совпадают, заменим f на эквивалентную функцию
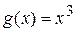 ,
, 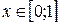 ,
,
( 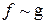 , так как
, так как 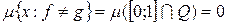 ).
).
Функция 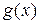 непрерывна и интегрируема по Риману, а значит и по Лебегу и имеет место равенство
непрерывна и интегрируема по Риману, а значит и по Лебегу и имеет место равенство
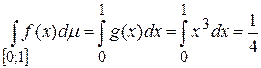 .
.
Задача 3. Вычислить интеграл Лебега от функции 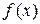 ,
,
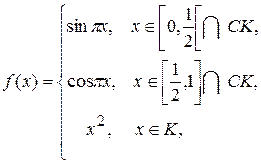
где 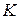 – канторово множество,
– канторово множество, 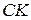 – его дополнение.
– его дополнение.
Решение.Функция 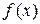 эквивалентна на отрезке [0; 1] функции
эквивалентна на отрезке [0; 1] функции 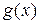
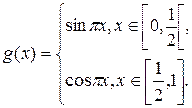
так как 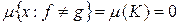 . Поэтому
. Поэтому
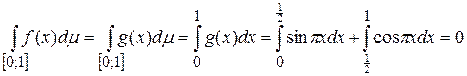 .
.
Задача 4. Вычислить интеграл Лебега от функции 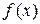 на отрезке [0; 1], если
на отрезке [0; 1], если 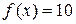 в точках канторова множества, а на смежных интервалах графиком функции служат треугольники, опирающиеся на эти интервалы, как на основания, высоты 1.
в точках канторова множества, а на смежных интервалах графиком функции служат треугольники, опирающиеся на эти интервалы, как на основания, высоты 1.
Решение.Воспользуемся аддитивностью интеграла Лебега и представим интеграл в виде суммы двух интегралов: первый по канторову множеству, он будет равен нулю, так как 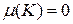 , а второй – по его дополнению.
, а второй – по его дополнению.
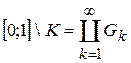 ;
; 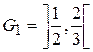 ,
, 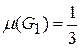 ;
; 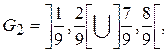
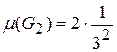 ;
;
и так далее.
Следовательно, 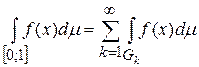 .
.
На каждом 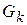 функция непрерывна и поэтому интегрируема по Риману. Интеграл Римана равен площади треугольника значит,
функция непрерывна и поэтому интегрируема по Риману. Интеграл Римана равен площади треугольника значит,
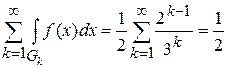 .
.
Задача 5. При каких значениях параметров 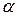 и
и 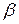 функция
функция 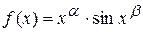 , xÎ]0,1[
, xÎ]0,1[
1) интегрируема по Лебегу,
2) несобственно интегрируема по Риману.
Решение.Неограниченная на отрезке [a;b] функция интегрируема по Лебегу в том случае, когда она абсолютно интегрируема по Риману в несобственном смысле.
1 случай: 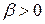 .
.
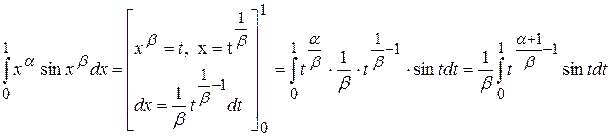 Данный интеграл сходится абсолютно, если
Данный интеграл сходится абсолютно, если 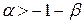 . Действительно, подынтегральная функция по модулю эквивалентна
. Действительно, подынтегральная функция по модулю эквивалентна 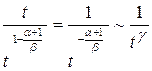 , следовательно
, следовательно 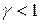 , то есть
, то есть 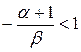 .
.
Итак, при 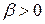 функция интегрируема по Лебегу при
функция интегрируема по Лебегу при 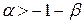 .
.
Для интегрируемости по Риману необходимо, чтобы интеграл сходился условно. Используя признак Дирихле, получаем
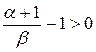 , следовательно
, следовательно 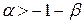 .
.
2 случай: 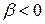 .
.
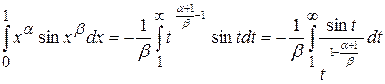 .
.
Интеграл сходится абсолютно, если 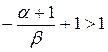 , то есть
, то есть 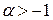 . Следовательно, при
. Следовательно, при 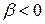 функция интегрируема по Лебегу, если
функция интегрируема по Лебегу, если 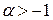 . Для интегрируемости по Риману необходимо, чтобы
. Для интегрируемости по Риману необходимо, чтобы 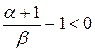 , следовательно
, следовательно 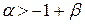 .
.
Итак, функция 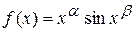 интегрируема по Лебегу при
интегрируема по Лебегу при 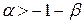 (
( 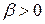 ) и
) и 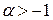 (
( 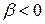 ); по Риману при
); по Риману при 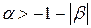 .
.
Задача 6. Вычислить интеграл Лебега по интервалу ]0,+¥[ от функции 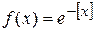 .
.
Решение.Интервал ]0,+¥[ – пространство с s-конечной мерой, так как 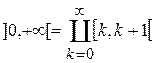 и m [k, k+1[ = 1 < +¥. На каждом полуинтервале [k, k+1[ функция
и m [k, k+1[ = 1 < +¥. На каждом полуинтервале [k, k+1[ функция 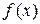 является простой, так как
является простой, так как 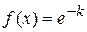 при x Î [k, k+1[.
при x Î [k, k+1[.
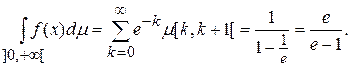 .
.
Задача 7. Исходя из определения интеграла Лебега, вычислить
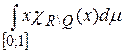 ,
,
где 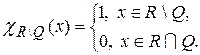 – характеристическая функция множества
– характеристическая функция множества 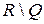 .
.
Решение.Построим для измеримой функции 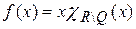 ,
, 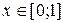 последовательность простых интегрируемых функций, равномерно сходящуюся на [0; 1] к
последовательность простых интегрируемых функций, равномерно сходящуюся на [0; 1] к 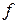 . А именно, для
. А именно, для 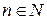 положим
положим 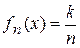 на множестве
на множестве 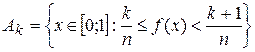 ,
, 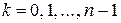 . Тогда последовательность
. Тогда последовательность 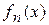 является искомой. Кроме того, поскольку
является искомой. Кроме того, поскольку 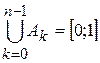 , то
, то 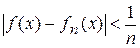 для
для 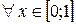 . Следовательно, последовательность равномерно сходится к
. Следовательно, последовательность равномерно сходится к 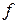 .
.
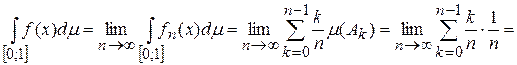
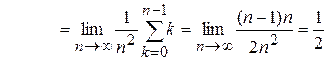 ,
,
так как 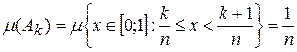 и поскольку множество
и поскольку множество 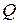 рациональных чисел имеет меру нуль.
рациональных чисел имеет меру нуль.
Задача 8. Найти предел
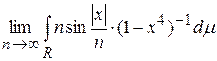 .
.
Решение.Рассмотрим функциональную последовательность
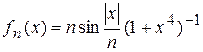 ,
, 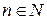 ,
, 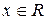 .
.
Для каждого 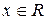
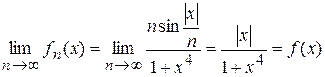 .
.
Кроме того, эта функциональная последовательность имеет мажоранту
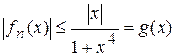 ,
, 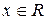 .
.
Неотрицательная функция g интегрируема по Риману в несобственном смысле, поэтому она интегрируема по Лебегу. Следовательно, по теореме Лебега f также интегрируема по Лебегу на R и справедливо равенство
 .
.
Задание 1. Выяснить, интегрируема ли по Риману, по Лебегу на отрезке [0; 1] функция f, если да, то вычислить интеграл Лебега.
1.1. 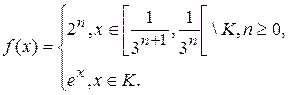
1.2. 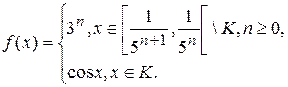
1.3. 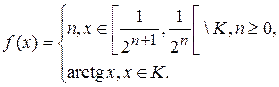
1.4. 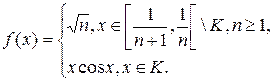
1.5. 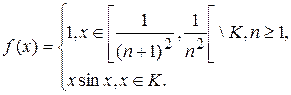
1.6. 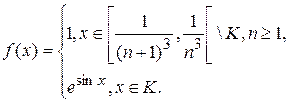

1.7. 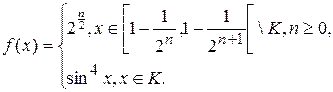
1.8. 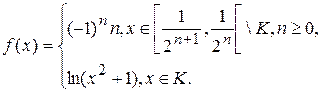
1.9. 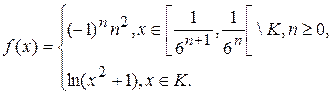
1.10. 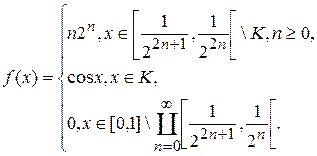
1.11. 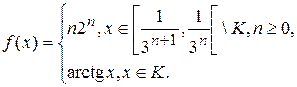
1.12. 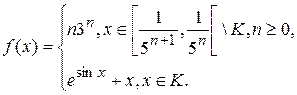
1.13. 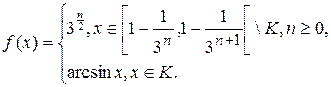
1.14. 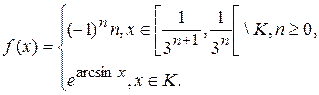
Задание 2. Для заданной функции 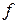 на отрезке [-1; 2]
на отрезке [-1; 2]
1) выяснить, является ли она ограниченной;
2) найти множество точек разрыва;
3) выяснить, существует ли для неё собственный или несобственный интеграл Римана;
4) вычислить интеграл Лебега, если он существует, воспользовавшись подходящей заменой на эквивалентную, имеющую меньшее множество точек разрыва.
2.1. 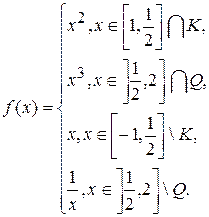
2.2. 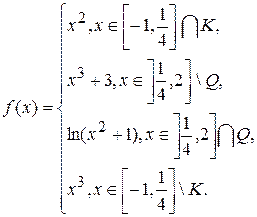
2.3. 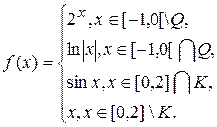
2.4. 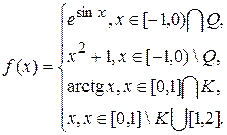
2.5. 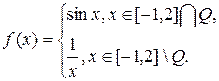
2.6. 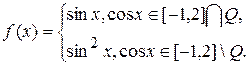
2.7. 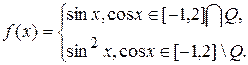
2.8. 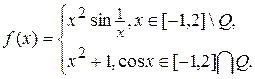
2.9. 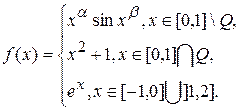
2.10. 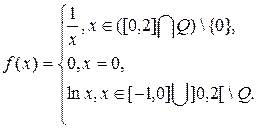
2.11. 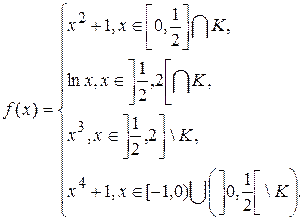
2.12. 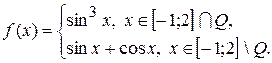
2.13. 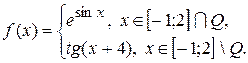
2.14. 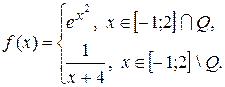
Задание 3. Для заданной последовательности функций 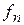 , определённых на множестве X, выяснить, какие из теорем о предельном переходе применимы. Найти и сравнить:
, определённых на множестве X, выяснить, какие из теорем о предельном переходе применимы. Найти и сравнить:
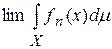 и
и 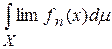 , если:
, если:
3.1. 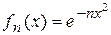 ,
, 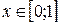
3.2. 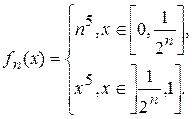
3.3. 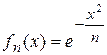 ,
, 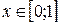
 3.4.
3.4. 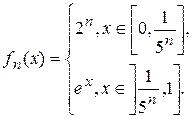
3.5. 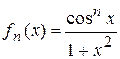 ,
, 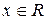
3.6. 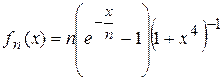 , xÎ[0,+¥[
, xÎ[0,+¥[
3.7. 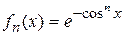 ,
, 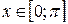
3.8. 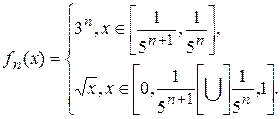
3.9. 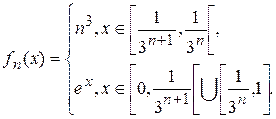
3.10. 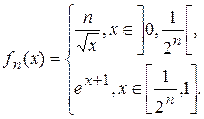
3.11. 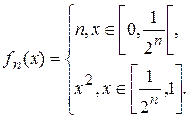
3.12. 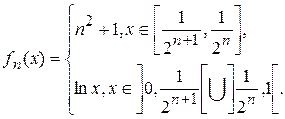
3.13. 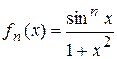 ,
, 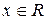
3.14. 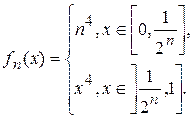
Дата добавления: 2021-07-22; просмотров: 715;











