ОСОБЕННОСТИ ЭКСПЛУАТАЦИИ СИНХРОННОГО КОМПЕНСАТОРА
Можно показать, что эффективность использования синхронного компенсатора зависит от исходного значения коэффициента мощности линии, в которой предполагается выполнить компенсацию реактивной мощности. Проиллюстрируем рассмотрение этого вопроса частным примером. Пусть генератор СГ работает на некоторую активно-индуктивную нагрузку (рис.5.11).
|
При этом потребитель П потребляет ток, имеющий активную составляющую Ia=1000 A
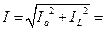 и индуктивную IL=1000 A. В этом случае потребляемый ток равен
и индуктивную IL=1000 A. В этом случае потребляемый ток равен
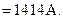
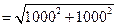 Коэффициент мощности линии (он же коэффициент мощности потребителя) cosφл = cosφп = Ia/I = 1000/1414 = 0,71.
Коэффициент мощности линии (он же коэффициент мощности потребителя) cosφл = cosφп = Ia/I = 1000/1414 = 0,71.
Для разгрузки генератора и линии от индуктивного тока у потребителя энергии поставлен синхронный компенсатор СК, который при некотором возбуждении берёт из сети ёмкостный ток Ic = 600 A. В этом случае индуктивный ток в линии генератора уменьшается до значения IL – Ic = 1000 - 600 = 400 A.
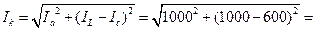 При этом ток в линии и в генераторе будет
При этом ток в линии и в генераторе будет
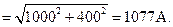
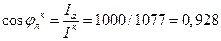 Коэффициент мощности линии с подключенным синхронным компенсатором
Коэффициент мощности линии с подключенным синхронным компенсатором
.
Ток в генераторе и линии за счет подключения синхронного компенсатора уменьшился на ∆Iл=1414-1077=337 А, что потребовало выработки синхронным компенсатором тока Ic=600 A.
Определяем эффективность использования синхронного компенсатора при повышении сosφл c 0,71 до 0,928 по отношению Кэф = ∆ Iл/ Ic = 337/600 = 0,56.
Оцениваем эффективность использования синхронного компенсатора при дальнейшем увеличении cosφл. Так, чтобы полностью освободить генератор и линию от индуктивных токов, потребуется выработка компенсатором ещё 400 А. При этом ток в линии уменьшается всего на 1077-1000=77 А.
Определяем эффективность использования синхронного компенсатора при повышении сosφл c 0,928 до 1 по отношению Кэф = ∆ Iл/ Ic = 77/400 = 0,19.
Выполним более детальное исследование синхронного компенсатора в рассматриваемой электрической сети.
 В качестве конечной цели указанного исследования поставим построение функциональной зависимости Кэф = f(cosφл).
В качестве конечной цели указанного исследования поставим построение функциональной зависимости Кэф = f(cosφл).
В рассматриваемой линии величины cosφл, Iа и Iр связаны следующими соотношениями
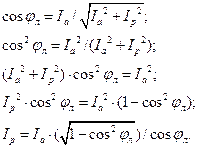 |
Результаты расчётов реактивной составляющей тока линии Ip сводим в таблицу 5.1.
Таблица 5.1
К расчёту коэффициента эффективности использования синхронного компенсатора
| № пп | cosφл | Iр, А | Iс, А | Iл, А | ∆Iл, А | Кэф | ∆Кэф |
| 1. | 0,75 | 0,686 | − | ||||
| 2. | 0,80 | 0,656 | 0,60 | ||||
| 3. | 0,85 | 0,626 | 0,60 | ||||
| 4. | 0,90 | 0,587 | 0,78 | ||||
| 5. | 0,95 | 0,537 | 1,00 | ||||
| 6. | 1,00 | 0,414 | 2,46 |
Представленная на рис.5.12 зависимость Кэф = f (cosφл) показывает, что по мере приближения cosφл к предельному значению, т.е. к единице эффективность использования синхронного компенсатора имеет тенденцию к интенсивному снижению.
Можно показать, что на участках значений cosφл, близких к единице, частные значения коэффициентов эффективности использования синхронных компенсаторов значительно ниже приведённых на рис.5.12. Из сказанного следует, что при решении проектных задач, предусматривающих выбор номинальной мощности синхронного компенсатора, следует соотносить выигрыш от уменьшения потерь в линии с затратами на устанавливаемый синхронный компенсатор.
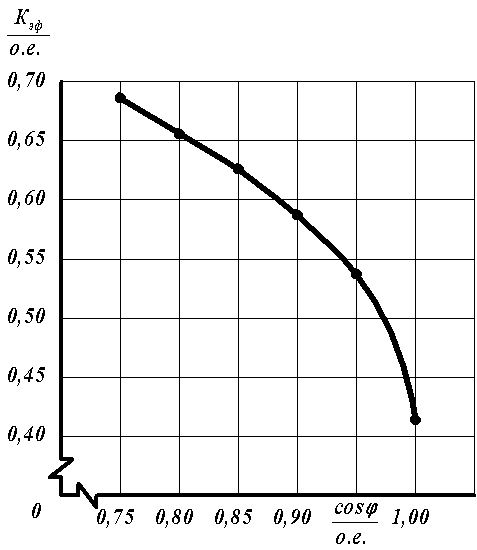
Рис.5.12. Зависимость коэффициента эффективности использования синхронного компенсатора от коэффициента мощности линии
В качестве предварительной оценки при выборе максимального значения коэффициента мощности линии, достигаемого с помощью использования синхронного компенсатора, следует учитывать интенсивность снижения эффективности применения синхронного компенсатора ∆Кэф. Расчётное соотношение имеет вид
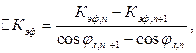 |
где n-порядковый номер расчётной точки зависимости Кэф = f (cosφл).
Например, при увеличении cosφл с 0,75 до 0,8 расчёт ∆ Кэф показывает
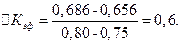 |
Дата добавления: 2017-06-13; просмотров: 1879;

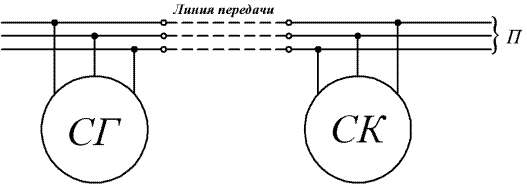 Рис. 5.11. Схема включения синхронного компенсатора
Рис. 5.11. Схема включения синхронного компенсатора










