Термодинамика компрессорного процесса

При работе компрессорных машин происходит сжатие газа с изменением его объема, давления и температуры. Для идеального газа в соответствии с уравнением Менделеева - Клайперона можно записать

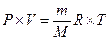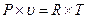, или (2.2)

где 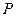- абсолютное давление газа, Па;

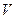- объем газа, м ;

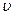- молярный объём, л/моль;

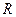- универсальная газовая постоянная, 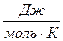; (8,31 Дж/мольК);

М – молярная масса, кг/моль;

- абсолютная температура, К.

Процессы сжатия газа в компрессорах удобно изображать на диаграмме давление – удельный объем ( ).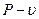

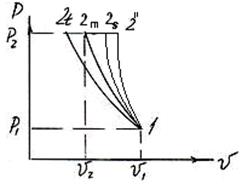
Рисунок 73 - Кривые сжатия газа

Исходный газ (состояние 1) давлением 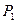с удельным объемом 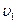подвергается сжатию до состояния 2 – до давления 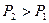; при этом удельный объем газа уменьшается до 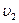. Одновременно изменяется температура от 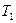до .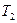

Ход кривой 1-2 зависит от условий сжатия.

Рассмотрим возможные методы компрессии газа.

1) Изотермическое сжатие. Процесс сжатия сопровождается разогревом газа. Чтобы температура была постоянной ( 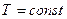), необходимо интенсивно отводить тепло. В случае изотермического сжатия ( 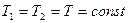) процесс изображается линией .

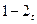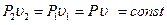. (2.3)

2) Для адиабатического сжатия (полная тепловая изоляция, нет подвода и отвода тепла, энтропия остается постоянной) процесс идет по кривой 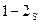; при этом

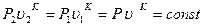, (2.4)

где 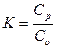- показатель адиабаты (для двухатомных газов К=1,4; для одноатомных К=1,67; для трехатомных К=1,3).

3) Для политропного процесса (когда 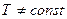, 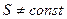) процесс идет по линии 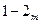. При этом

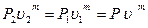. (2.5)

В реальных условиях всю теплоту (выделенную) отвести не удается из-за ограниченной поверхности теплосъема. Поэтому реальный процесс сжатия идет по линии 1-2'', т.е. с показателем политропы m>k.

При эксплуатации компрессоров нужно знать температуру газа 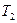после компрессора. Запишем уравнение Менделеева – Клайперона для исходного газа и сжатого газа

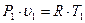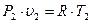и (2.6)

и найдем соотношение температур

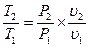. (2.7)

Для политропного процесса

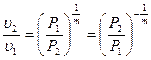. (2.8)

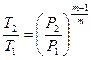. (2.9)

Тогда

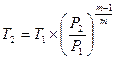. (2.10)