ФОРМАЛИЗАЦИЯ И СТАТИСТИЧЕСКИЕ ШКАЛЫ.

Любые наблюдаемые явления представляют собой эмпирическое множество фактов, с которыми напрямую, порой, не удается провести никаких операций (макрокосм, микромир и так далее). Тем не менее, при попытке начала операции измерения можно определить существование двух и только двух, видов отношений на этом множестве.

Первый вид: эквивалентность - J.

Второй вид: предпочтение -П.

Для возможности измерений, чем занимается теория планирования эксперимента, необходимо перейти к числовому множеству, отражающему эмпирическое множество в виде чисел и отношений в числовом множестве, тогда эквивалентности в эмпирическом множестве будет соответствовать равенство или тождество в числовом множестве; а предпочтению в эмпирическом множестве отношения больше или меньше в числовом (Л.4).

Таким образом мы имеем два множества: эмпирическое- Э, с отношениями на нем и числовое - N, с отношениями на нем. Причем, каждому элементу эмпирического множества Э_i (i =1,…N) соответствует элемент числового множества Ч_i (i= 1,…N).

Теперь необходимо найти функцию f(x):- гомоморфную, работающую в одном направлении или изоморфную, работающую в обеих направлениях, переводящую члены одного множества в другое.

Таким образом, упорядоченное статистическое множество (кортеж), состоящий из трех членов: эмпирического множества Э, числового множества N, функции f(x), называется статистической измерительной шкалой. В квалиметрии и теории качества этот кортеж носит название квалиметрической или измерительной шкалы.Примерное представление об элементах статистической измерительной шкалы представлено на рис.9.

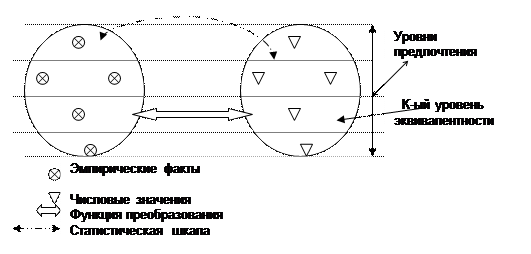
Рис.9. Представление о статистической шкале

Следует отметить, что, привычная всем шкала любого измерительного прибора не является статистической измерительной шкалой, а представляет собой числовое отображение функции f(x).

Мир шкал велик, существуют различные классы шкал, в том числе и многомерные шкалы, шкалы для различных топологических пространств и структур, рассмотрение которых не входит в круг задач пособия.

Далее рассмотрим основные виды шкал, применяемых в стандартных измерениях. Единственное, что нужно понять и запомнить: любое измерение осуществляется в какой – либо шкале! Причем выбор шкалы влияет на правильность измерений.

Так же как выпуск денежной массы, не обеспеченной товарами, приводит к инфляции и последующей девальвации денежной единицы, также и неверный выбор шкалы обесценивает процесс измерения в ходе эксперимента.

А) Шкала эквивалентности - ШЭ

Данная шкала в разных литературных источниках может носить разное название, имея при этом, одинаковый смысл: шкала - номинальная, порядка, эквивалентности, классификационная, наименований, (два последних названия представляются не корректными, что будет видно из дальнейшего изложения), толерантная. Разберемся с логической основой шкалы эквивалентности. Пусть, проводится такое измерение, когда каждому объекту может быть приписано любое значение, но обязательно каждому несхожему объекту свое конкретное значение, что соответствует использованию любой монотонной функции. Набор объектов, имеющих одинаковые значения, приводит к шкале эквивалентности. Например, при выпуске продукции, часть ее бракуется, образуя подмножество Т, эквивалентное в заданном нами смысле, где t₁, t₂,…Î T. Виды брака могут быть разными, но они едины с позиций контролера. Подобная ситуация представлена на рис.10. На рисунке для наглядности и возможности сравнения приведены все типы рассматриваемых в пособии шкал.

Рис.10. Смысл статистических шкал

Шкала эквивалентности может быть разделена на две подшкалы:

а) подшкала наименований, – все полученное подмножество Т, со свойственными ему аксиомами, которые кратко представлены ниже:

1. Если t Î T, а t J t , то получаем свойство изоморфности, когда любой элемент равен сам себе.

2. Если t₁, t₂ Î T, а t₁ J t₂, то и t₂ J t₁ , то получаем свойство симметрии.

3. Если t₁,t₂,t₃ ÎT, а t₁ J t₂ и t₂ J t₃, то t₁ J t₃ , то получаем известное из школьной математики свойство транзитивности,- когда два элемента порознь равны третьему, то они равны между собой.

б) подшкала классификаций. Разделим Т (полученное подмножество) на классификационный показатель J, частное Т/J создает непересекающиеся области в Т, имеющие одинаковый показатель эквивалентности.

На рис.10 А) подмножество брака - Т, может содержать разные виды брака. Например, при контроле качества на телевизионном производстве это может быть: скол на фанеровке, несведенные лучи, трещина на кинескопе и т.п. Все эти дефекты эквивалентны по одному признаку - невозможности поставки в торговую сеть из-за обнаруженных несоответствий ТУ. Второй пример, участники первенства премьер - лиги России по футболу (в начале сезона) разделены на команды, имеющие разные цвета на футболках, но их объединяет единый признак эквивалентности - участие в первенстве России.

Логику измерений по шкале эквивалентности можно отразить следующим образом:

Q_i = Q_зад или Q_i 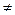Q_зад , 1

где: Q_i - характеристика измеряемого объекта,

Q_зад- требования ТУ или иных документов.

Отметим, что подмножество Т не вводит никаких числовых значений и не определяется никакими параметрами. Поэтому ШЭ относится к разряду непараметрических шкал.