Реализация звеньев второго порядка

В общем виде выражение передаточной функции ФНЧ второго порядка для фильтров полиноминального типа можно записать так:

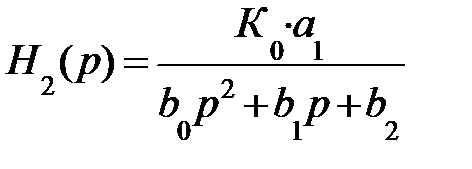(9.27)

При а₀ = 0. А для дробного типа, т.е. при наличие нулей в полосе не пропускания (например: инверсные Чебышева):

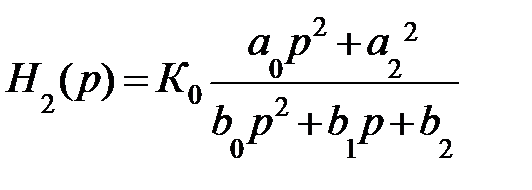(9.28)

На рисунке 9.52 представлена схема ARC - фильтра нижних частот второго порядка с отрицательной обратной связью.

Рис. 9.52 Активный фильтр нижних частот второго порядка с отрицательной обратной связью

Для узловых напряжений U₃ и U₄ на основании законов Киргхофа можно записать:

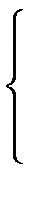
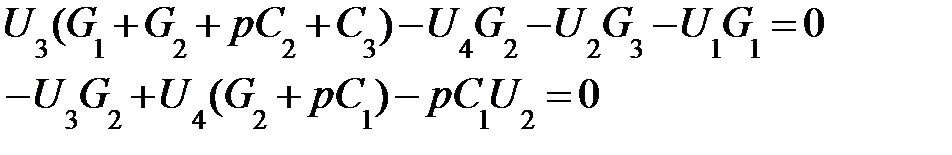(9.29)

Учтем, что U₄ = - U₂/μ и тогда получим:

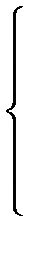
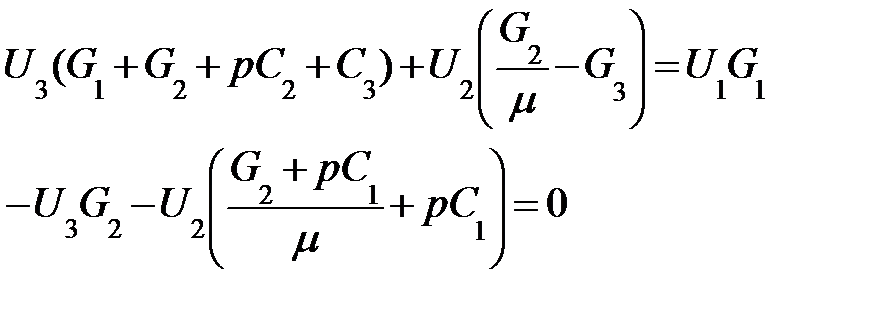(9.30)

Для решения этой системы можно использовать MathCAD. На рисунке 9.53 приведен листинг программы решения системы уравнений с помощью встроенной функции Find (x,y…)

Рис. 9.53 Листинг программы

В блоке Given (Заданно) записывается система уравнений (например, (9.30)), далее указываются, если необходимо, коэффициенты системы и вызывается функция Find(--) решения системы уравнений с указанием неизвестных в качестве аргумента. В данном примере под U₂ подразумевается коэффициент передачи H₂(p) = U₂/U₁. Для решения системы уравнений в символическом виде необходимо на панели инструментов инициализировать значок символические операторы и затем символический знак равенства ( → ).

С учетом того, что μ→ ∞ получим:

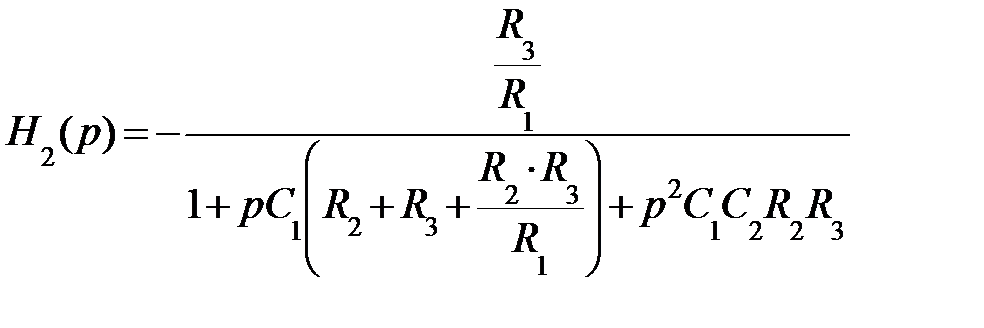
Приравняв коэффициенты этой функции с коэффициентами выражения (9.27), получим: a₀ = 0, a₂ =1, K₀ = - R₃ / R₁ , b₂ = 1, b₀ = C₁C₂R₂R₃, b₁ = C₁(R₂+R₃+( R₂R₃/R₁).

Как видно, расчетные формулы справедливы для произвольных положительных значений коэффициентов a_i и b_i. Таким образом, задавая эти значения для конкретных типов фильтров (Баттерворта, Чебышева, Гаусса), можно реализовать эти фильтры по одной схеме. Коэффициент передачи постоянного сигнала K₀ фильтра оказывается отрицательным, поэтому прошедший через фильтр низкочастотный сигнал будет инвертирован. Для расчета фильтра можно, например, задать значение сопротивлений R₁ и R₃ и по приведенным формулам вычислить значение R₂ , C₁ и C₂.

Однако чтобы реальная схема фильтра имела желаемую амплитудночастотную характеристику, входящие в неё элементы могут быть подобранны исходя из следующих соображений. При подборе сопротивлений никаких проблем не возникает, поскольку их стандартные номиналы задаются с однопроцентным допуском. Что касается конденсаторов, то допуск их номинальных значений, как правило, составляет 10% и более. В связи с этим лучше при расчете фильтра задавать значение емкостей конденсаторов и вычислять необходимые значения сопротивлений. Поэтому решим уравнение относительно сопротивлений.

С₂ ≈ 10/f_c [мкФ]; С₁ ≤ С₂; ;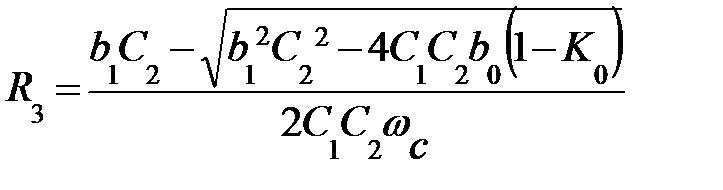

; .

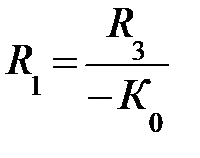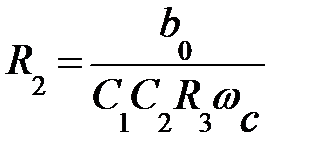Для того, чтобы получить сопротивление R₃ было действительным, должно выполняться условие:

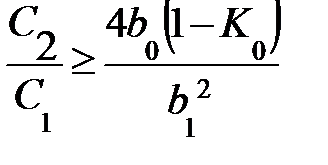
При выполнении этого условия в процессе расчета фильтра не следует выбирать отношение C₂/C₁ много большим величины, стоящей справа.

Фильтр нижних частот на ОУ с положительной обратной связью может быть реализован по схеме приведенной на рис. 9.54.

Рис. 9.54 Фильтр НЧ с ПОС

Запишем уравнения для напряжений в узлах 3 и 4:

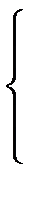
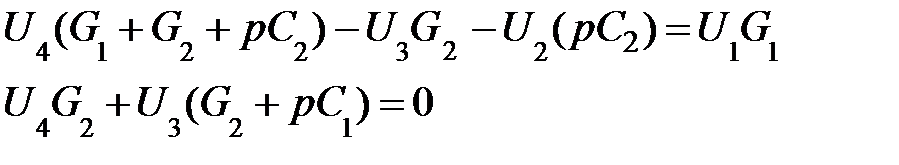
При этом U₃ = U₂/K₀ , а K₀ = 1 + R₄/R₃. С учетом этого система уравнений примет вид:

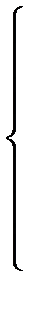
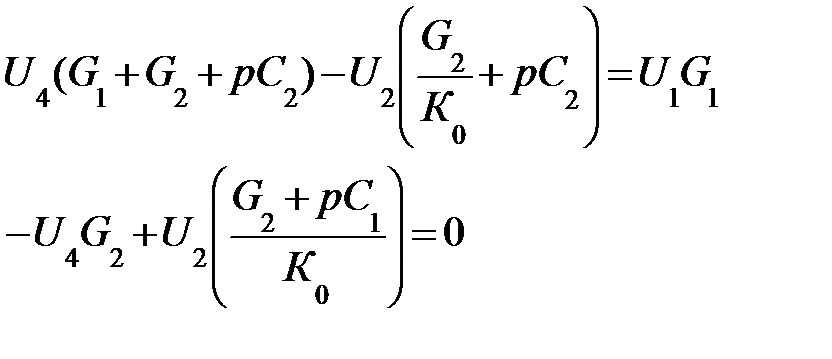
Воспользовавшись программой, листинг которой приведен на рис. 11.55, получим выражение коэффициента передачи:

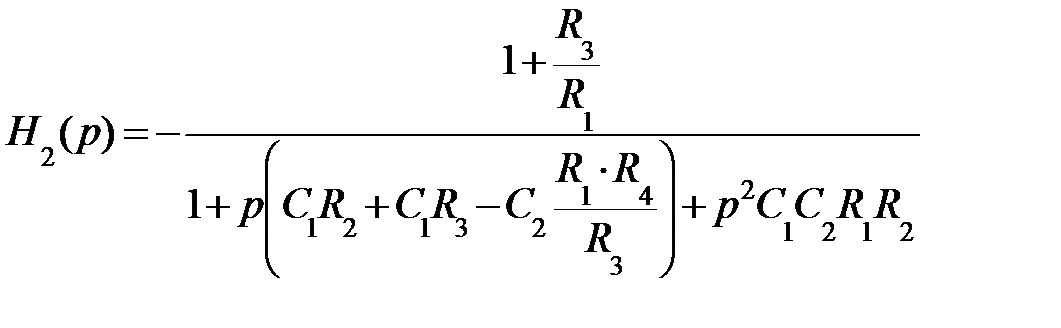
Сравнивая это выражение с уравнением (9.27) находим значение элементов схемы: К₀ = 1 + R₄ / R₃ ; 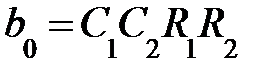; ; 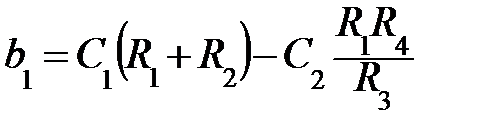a₁ = 1; 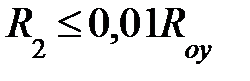, где 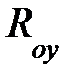входное сопротивление используемого операционного усилителя.

; ; ; ;

; ;

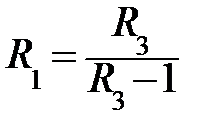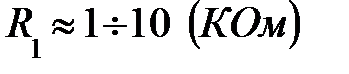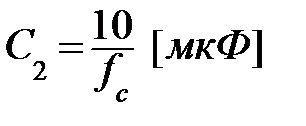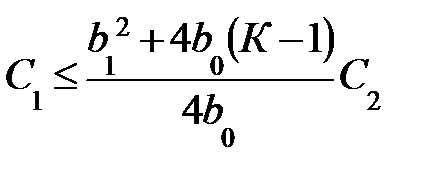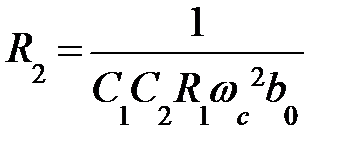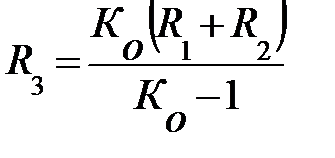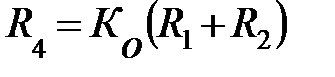
Если К_о=1, то R₃ → ∞, а R₄ = 0. Расчеты можно упростить если положить R₁ = R₂ = R и C₁ = C₂ = C. Тогда 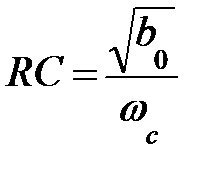; 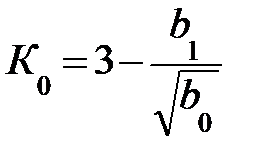, причем 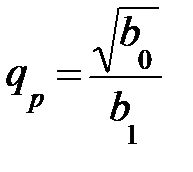–есть добротность полюсов звеньев фильтра.

Если заменить в схеме на рис. 9.52 сопротивление на емкости и наоборот, то получится ФВЧ второго порядка с отрицательной обратной связью (рис. 9.56).

Рис. 9.56 Активный фильтр верхних частот второго порядка с отрицательной обратной связью

Чтобы записать выражение передаточной функции для фильтра верхних частот второго порядка, нужно по формуле (9.27) в соответствии с преобразованием частот вместо p подставить 1/p. Тогда:

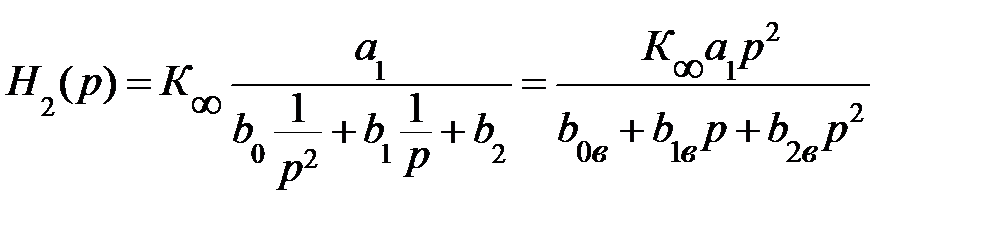(9.31)

При этом полиномиальные коэффициенты знаменателя связаны с подобными коэффициентами ФПНЧ следующим образом:

b_2в = b₀ ; b_1в = b₁ ; b_0в = b₂

По аналогии с ФНЧ второго порядка можно получить передаточную функцию для этого фильтра:

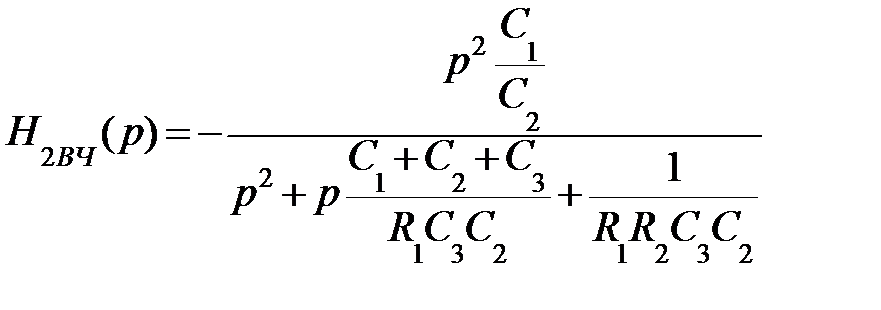(9.30)

Сравнивая выражения (9.29) и (9.30) находим коэффициент передаточной функции для ФВЧ:

К_∞ = – С₁ / С₂; a₁ = 1; b_2в = 1; ;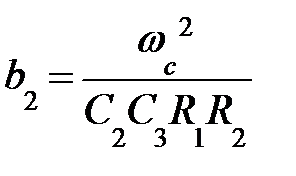

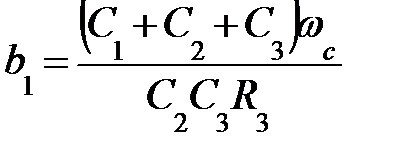
Положим 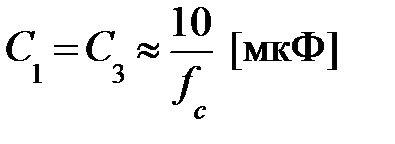, тогда С₂ = С₁ / К_∞ и приняв, например, R₂ = 1 Ком, легко найти оставшиеся элементы схемы.

Активный фильтр верхних частот на ОУ с положительной ОС показана на рис. 9.57.

Рис. 9.56 Активный фильтр верхних частот второго порядка с положительной обратной связью

Его передаточная функция имеет вид:

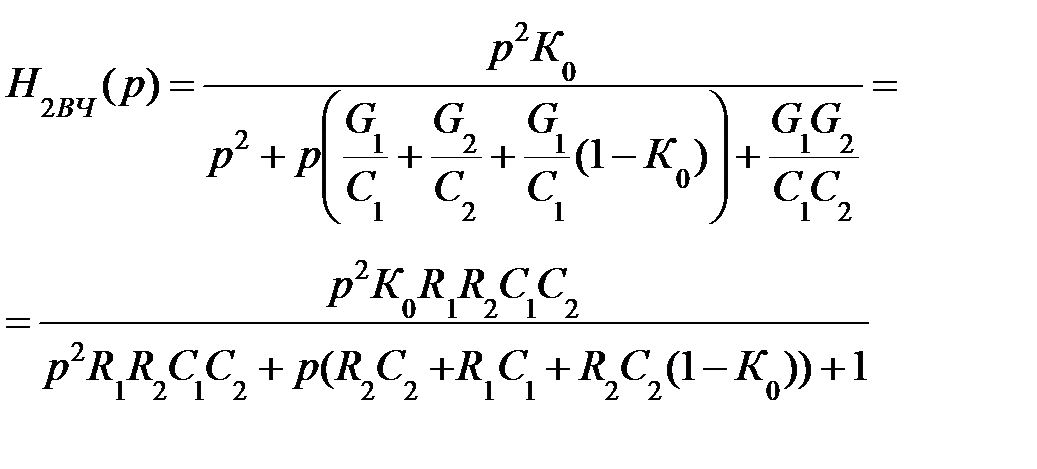
Элементы схемы можно найти следующим образом:

К₀ ≥ 1; К₀ = 1 + R₄/R₅ ; R₅ ≤ 0,01 R_оу; 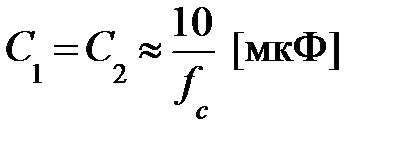; b_2в = ;

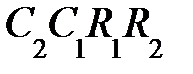b_2в = ; ; ;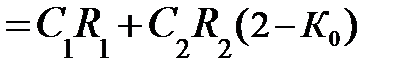

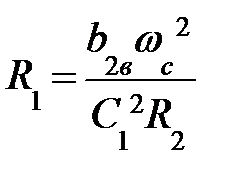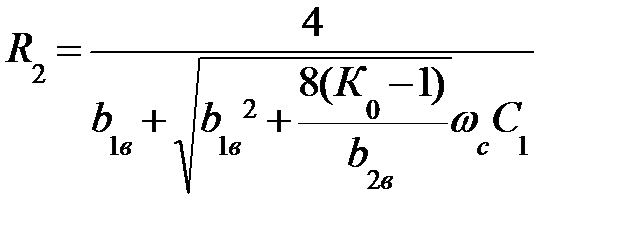(или R₂ = R₁ / К₀). Для упрощения расчетов можно положить C₁ = C₂ = C.

Из вышеизложенного видно, что коэффициент усиления фильтра не зависит от частоты среза. Существенным недостатком фильтров с положительной ОС является необходимость тщательной подборки коэффициента усиления, так как усилитель может переходить в режим возбуждения. Зато для построения фильтров различного типа достаточно изменить лишь значение коэффициента усиления при одних и тех же значениях элементов схемы.

Для увеличения избирательности фильтров применяют фильтры более высокого порядка. Для этого используют, как указывалось выше, цепочечное соединение звеньев первого и второго порядков. Еще одним путем увеличения избирательности является переход на фильтры дробного типа (например, инверсный Чебышева). Т.е. построение фильтров с нулями передачи в полосе запирания. Для таких фильтров общий вид передаточной характеристики приведен в формуле (9.28).

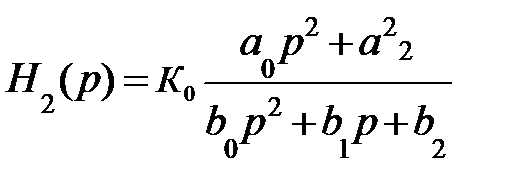
При реализации такой характеристики ARC-фильтров используют ОУ, в цепи ОС которых включают двойные Т-образные мосты (рис. 9.58).

Рис. 9.57 Активный фильтр с двоичным Т–образным мостом

Запишем напряжения для узлов 3, 4, 5:

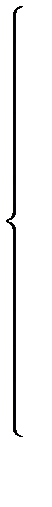
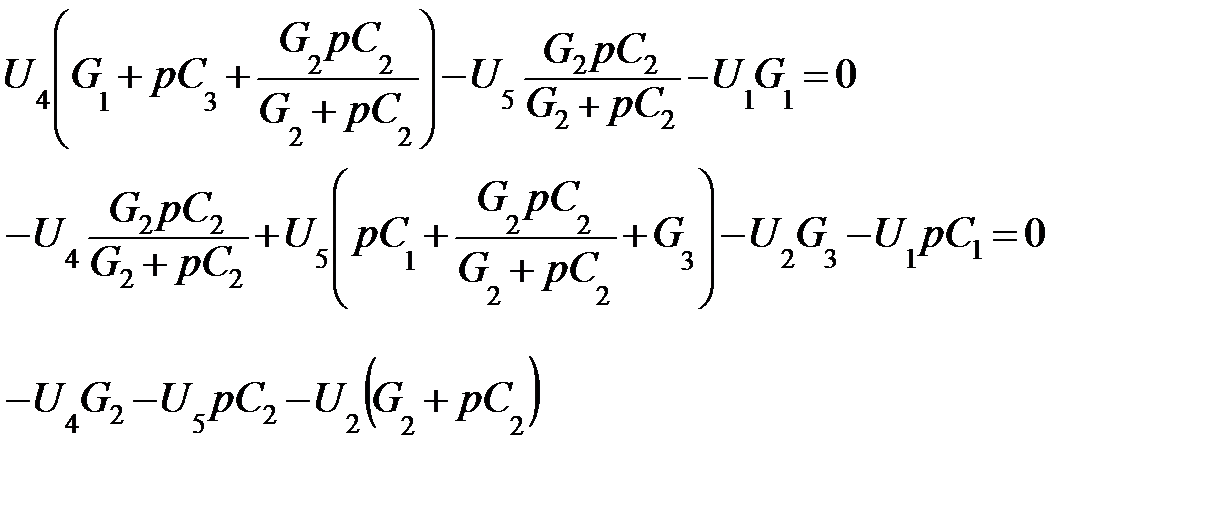
Воспользовавшись программой MathCAD, решаем систему в символьном виде. Решение будет выглядеть существенно громоздким. Поэтому для упрощения выражения примем:

; ; ; ;

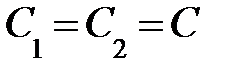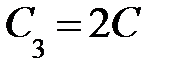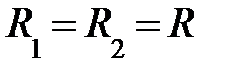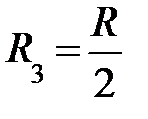Результат представлен листингом программы, показанном на рис. 9.59.

Таким образом, функция передачи для звена ARC-фильтра, изображенного на рис. 19.58, примет вид:

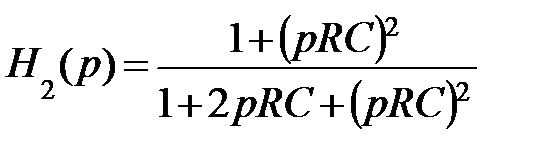
Сравнивая это выражение с формулой (9.28) получим:

К₀=1; а₂=1; b₂=1; b₁ = RC; a₀ = (RC)²

Значения элементов можно определить следующим образом:

; ;

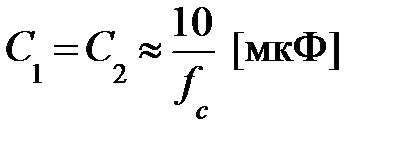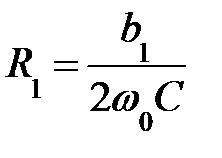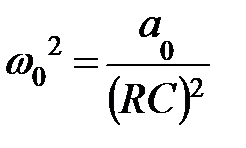
Можно емкости оставить теми же, а сопротивления взять разными:

R₁ = R ; R₂ = α·R ; ,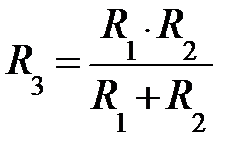

тогда функция передачи примет вид:

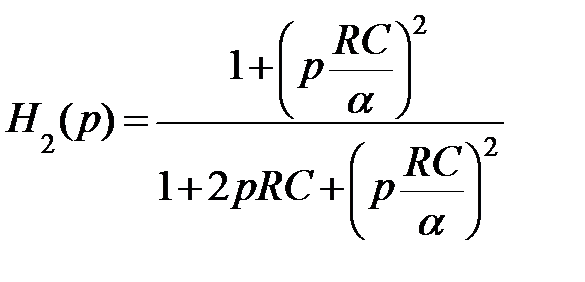
Для увеличения добротности фильтра ОУ можно включить в режиме с конечным усилением К₀ (рис. 9.60).

Рис. 9.58ARC-фильтр с двойным Т-образным мостом и коэффициентом усиления К₀ > 1

Его функция передачи будет описываться следующим выражением:

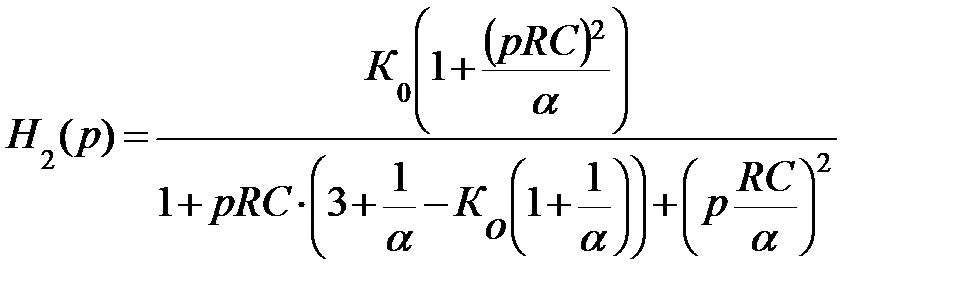
Более сложный вариант ARC-фильтра на двойном Т-образном мосте приведен на рис. 9.61.

Рис. 9.59 ARC-фильтр на двойном Т-образном мосте

Для упрощения конечного выражения функции передачи будем полагать:

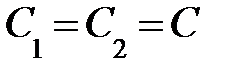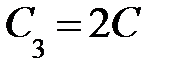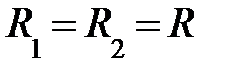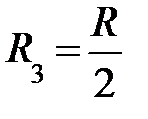; ; ; ; R₄ = β·R ;

C₄ = β·C ;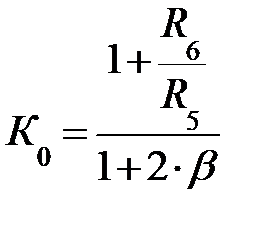

Тогда выражение для функции передачи примет вид:

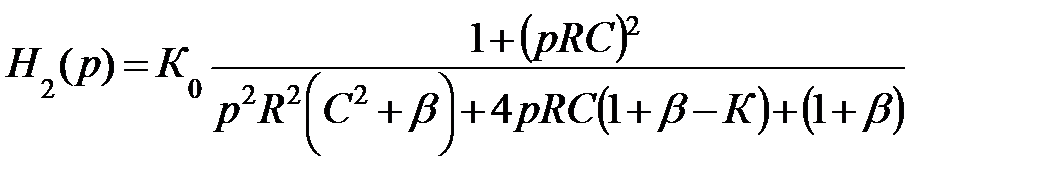
На рис. 9.62 приведен листинг программы для получения этой передаточной функции.

Примерные значения элементов схемы могут быть найдены следующим образом:

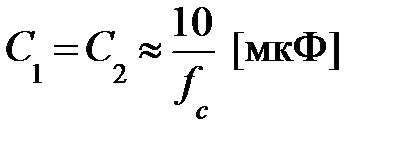; β = (0,5 ÷ 10); ;

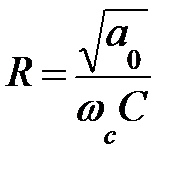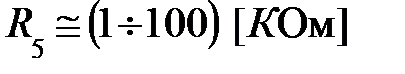
Далее приводится модуль программы расчета НЧ ARC-фильтра. Программа может быть использована для расчета трех типов фильтров: Баттерворта, Чебышева и инверсного Чебышева. Следует учесть, что данной программой можно пользоваться только при добротности звеньев фильтра не более 10. При большей добротности лучше строить звенья по более сложным схемам с использованием двух ОУ в каждом звене.

Подводя итог вышеизложенному, порядок расчета ARC-фильтров может быть таким:

1. По переходным данным выбираем тип аппроксимирующей функции Чебышева, Баттерворта, инверсный Чебышев и т.п.

2. Производится нормирование частот и определяется необходимый порядок ФПНЧ:

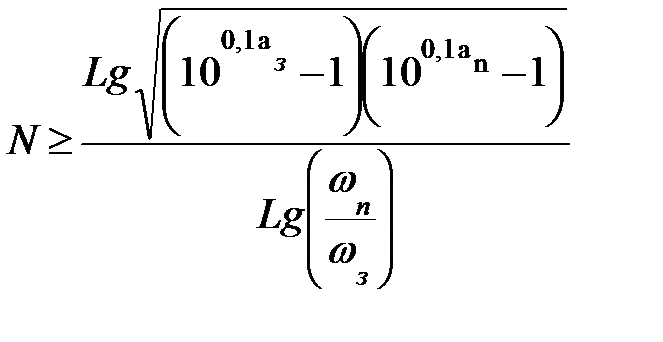– для фильтров Баттерворта;

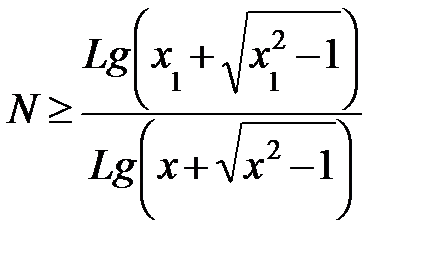– для фильтров Чебышева,

где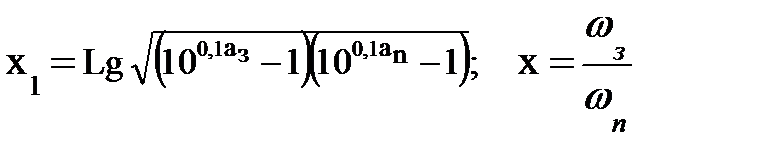

3. Вычисляются координаты нулей и полюсов передаточной характеристики ФПНЧ. Затем по таблице 9.7 эти координаты пересчитываются для проектируемого типа фильтра.

4. В соответствии с полученными координатами полюсов конструируется теоретическая функция передачи фильтра, которая представляется в виде произведения функций не выше второго порядка.

5. Выбирается схема реализации звеньев фильтра и рассчитываются элементы схемы.

6. Затем выбираются номиналы элементов схемы и осуществляется АЧХ фильтра.