Характеристика направленности как целевая функция

Прежде всего, следует отметить, что соотношение (10.4) фактически представляет собой преобразование Фурье от функции возбуждения 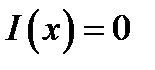везде, где 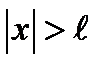. В этом случае характеристика направленности антенны приобретает вид:

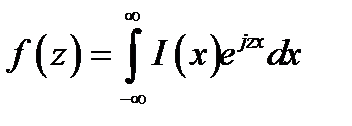(10.6)

Чтобы функция 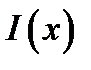допускала преобразование (10.6), она должна интегрироваться с квадратом на интервале (- ∞,+∞), давать полную мощность, и иметь конечное число минимумов и максимумов в пределах любого интервала. Эти же ограничения справедливы и для функции 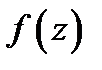, для которой обратное преобразование Фурье будет таким:

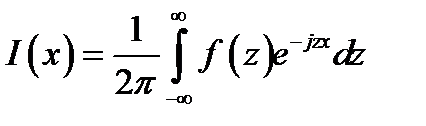(10.7)

Характеристика направленности 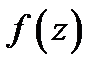, или функция преобразования Фурье имеет ограниченный спектр, в силу того, что функция возбуждается 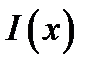определена только на интервале 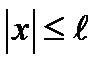, что существенно сужает класс функций 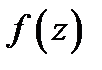. Причем эти целые функции представляют собой на комплексной плоскости (z),в ограниченной области, аналитические функции конечной степени, не превосходящей 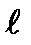. Число 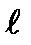называется степенью или типом функции и определяется как .

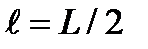Примером целой функции может быть функция вида 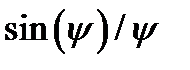, здесь 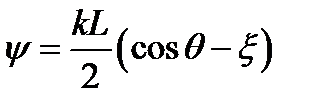, или .

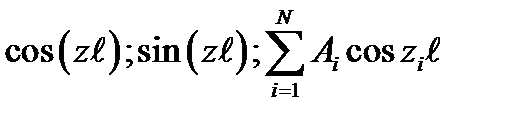Таким образом, множитель направленности линейного излучателя длиной 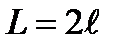является целой функцией степени, не превышающей значения 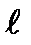. Это же утверждение справедливо для более сложных систем. В принципе, с помощью линейной системы длиной 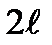можно реализовывать множитель направленности в виде любой наперед заданной непрерывной функции.