Ограничитель (пикосрезатель) Компрессор

Амплитуда входного сигнала в dB:

Амплитуда входного сигнала в В:

Входной сигнал рассчитывается по формуле:

Рис. 8.1 Форма периодического входного сигнала

Амплитудная характеристика устройств:

а) б)

Рис. 8.2 Амплитудные характеристики ( а- ограничителя, б- сжимателя )

Форма сигнала на выходе устройств:

а) б)

Рис. 8.3 Сигнала на выходе: а- ограничителя, б- сжимателя

Для расчета коэффициента гармоник сигнала на выходе устройств, сигнал можно представить в виде ряда Фурье:

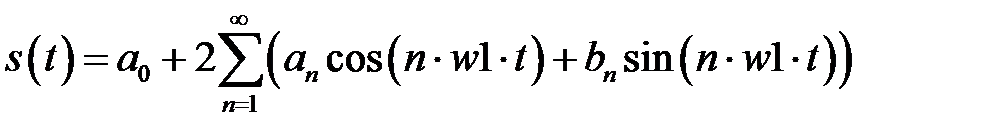
где а₀ - постоянная составляющая (для расчета коэффициента гармоник ее можно не учитывать);

а_n и b_n - коэффициенты ряда Фурье, которые рассчитываются по следующим формулам:

Для ограничителя:

Для компрессора:

Тогда амплитуду гармоник можно рассчитать по формулам:

Рис.8.4 Амплитуда гармоник на выходе: а- ограничителя, б- сжимателя

Коэффициент гармоник для i-го уровня входного сигнала

рассчитывается по формулам:

Рис. 8. 5 Коэффициент гармоник

Как видно из рисунка с увеличением уровня входного сигнала нелинейные искажения возрастают. При компрессировании сигнала больших уровней они существенно меньше, чем при ограничении.

Следует учитывать вероятность появления того или иного уровня сигнала, т.к. в появление сигнала с большим уровнем равно как и с маленьким маловероятно. Поэтому необходимо ввести коэффициент, характеризующий вероятность появления того или иного уровня сигнала.

Распределение уровней во времени реальных вещественных сигналов (как речевых, так и музыкальных) зависит не только от типа программ и длительности времени анализа, но и весьма существенно от выбранной весовой функции, учитывающей влияние на слуховой аппарат послезвучаний (звучаний, удаленных от текущего момента времени в прошлое) [10].

На рис. 8.6 приведена функция распределения уровней во времени, полученная экспериментальным путем [11] при исследовании записанных на магнитной ленте музыкальных и речевых отрывков сигналов звукового вещания. Существенное отличие этой зависимости от гауссовской наблюдалось лишь в области малых уровней, отличающихся от номинального значения (N = 0 дБ) более чем на 35 дБ. Поэтому с достаточным для практики приближением можно считать, что распределение уровней во времени подчиняется гауссовскому закону с параметрами:

Рис. 8.6 Функция распределения уровней

Вероятность того, что коэффициент гармоник превысит то или иное значение, равна произведению коэффициента гармоник для заданного уровня сигнала на вероятность его превышения. Для наглядности зависимости реального коэффициента гармоник от уровня входного сигнала изображены на одном рисунке в едином масштабе.

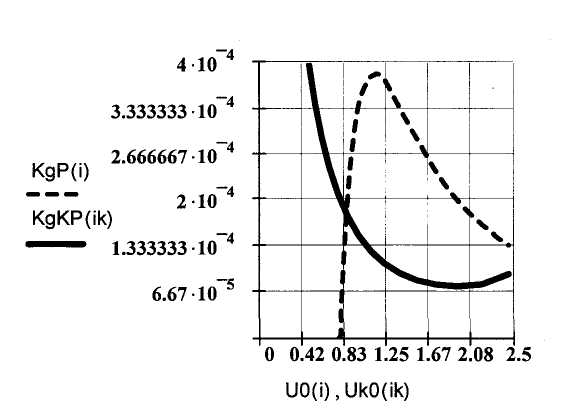
Рис. 8.7 Коэффициент гармоник с учетом вероятности появления уровней сигнала

Анализ нелинейных искажений звуковых сигналов на входе цифровых трактов (до АЦП) показывает эффективность применения компрессии входного сигнала в верхней части его динамического диапазона. Это позволяет уменьшать нелинейные искажения сигналов больших уровней и устранить потерю высокочастотных составляющих. Выбор оптимального закона компрессии позволит уменьшит нелинейные искажения (по сравнению с полученной оценкой).

Вопросы для самоконтроля

1. Какой метод расчета спектра на выходе нелинейных устройств рассмотрен в комплексе?

2. Оценка каких искажений и каким методом проведена в разделе 8?