Обработка результатов многократных прямых измерений

Рассмотрим серию из n прямых равноточных измерений физической величины 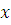, подчиняющейся нормальному закону распределения. Оценкой рассеяния однократных наблюдений относительно среднего арифметического 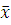является среднеквадратичная погрешность σ , определяемая по формуле:

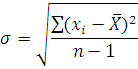
(6)

где х_i – однократное измеренное значение, n – число измерений в серии,

Выполнив серию из m измерений величины Х, мы получили бы новое значение среднего арифметического 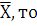есть новое действительное значение измеряемой величины. Повторив многократно серии измерений, мы убедимся в рассеянии средних арифметических значений. Характеристикой этого рассеяния является среднеквадратическое отклонение среднего арифметического 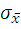, определяемого по формуле

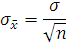
(7)

Величина 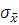используется для нахождения интервальной оценки погрешности многократных измерений одной и той же физической величины Х, истинное значение которой Х₀ неизвестно.

Теория показывает, что если рассеяние результатов измерений Х_i в серии подчиняется нормальному закону, то их погрешности , а так же среднее арифметическое, являясь случайной величиной, тоже подчиняется нормальному закону (распределение Гаусса) при достаточно большом числе измерения (n>50).

Причём мерой рассеяния 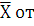истинного значения измеряемой величины служит 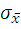, а доверительный интервал 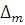при заданной доверительной вероятности Р определяется как 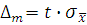. При это считается что истинное значение измеряемой величины лежит в границах 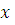= 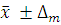Коэффициент t для нормального закона распределения случайной величины 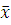находится по таблице интеграла Лапласа.

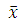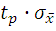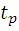При небольшом числе измерений (серия малой выборки) среднее арифметическое подчиняется закону распределения Стьюдента. При этом Δ_m= , где - коэффициент Стьюдента, который зависит от числа наблюдений n, выбранной доверительной вероятностью P, и находится по специальной таблице. Особенностью этого распределения является то, что доверительный интервал Δ_m с уменьшением числа наблюдений расширяется, по сравнению с нормальным законом распределения при той же доверительной вероятности P. Коэффициент 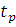распределения Стьюдента зависит от числа наблюдений и выбранной доверительной вероятности и находится по специальной таблице. Так при числе измерений n=14 и доверительной вероятности Р=0,95 коэффициент 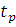=2,16.

Правила обработки прямых многократных измерений учитывают следующие факторы:

• обрабатываются результаты конечной серии из n измерений физической величины Х;
• результаты измерений Х_i могут содержать как случайную, так и систематическую погрешности;
• в серии могут встречаться грубые ошибки или промахи;
• распределение случайных погрешностей может отличаться от нормального

Обработка результатов многократных измерений должна осуществляться по следующему алгоритму:

1. Исключить известные систематические погрешности (например методическую погрешность) из результатов измерений (введением поправки).

2. Вычислить среднее арифметическое 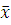из исправленных результатов измерений, принимаемое за действительное значение измеряемой величины.

3. Вычислить среднеквадратичное отклонение (СКО) результатов измерений σ.

4. Проверить наличие в группе наблюдений грубых погрешностей (промахов), исходя из того, что при нормальном законе распределения f(Δ) ни одна абсолютная погрешность 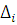= 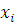- 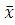случайного характера с вероятностью Р=0,997 не может выйти за пределы ±3σ. Наблюдения, не удовлетворяющие этому критерию, исключаются из группы и снова повторяют вычисления 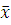и σ.

5. Вычислить оценку 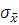по формуле (7).

6. Проверить гипотезу о том, что результаты измерений 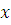, а также абсолютная погрешность принадлежат нормальному распределению.

Приближенно это можно сделать по критерию 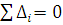, или построив гистограмму. Строго это определяется с использованием критериев Пирсона, Мизеса-Смирнова и др. При n<15 нормальность распределения не проверяется (распределение Стьюдента).

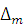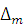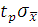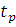7. Вычислить доверительные границы случайной погрешности результата измерения при заданной доверительной вероятности Р, =± , где коэффициент Стьюдента.

8. Вычислить границы, суммарной неисключенной систематической погрешности (НСП) средства измерений, которая складывается из основной и дополнительных.

При суммировании эти составляющие рассматриваются как случайные величины. При отсутствии данных о виде распределения не исключенных составляющих систематических погрешностей их распределения принимают за равномерные. При равномерном распределении НСП различного характера, границы (предельные значения) неисключенной систематической погрешности результата измерений 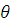вычисляют по формуле:

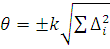, где i=0 соответствует основной НСП инструментального характера, k зависит от заданной доверительной вероятности Р (при Р=0,995, k=1,1). Для i=1 вычисляется дополнительная погрешность инструментального характера от влияющего фактора №1 (например температура)

9. Вычислить доверительные границы погрешности результата измерений для случаев:

Если 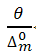<0,8, то не исключенной систематической погрешностью можно пренебречь и принять границы погрешности равным
=

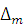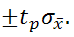
Если 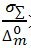>0,8 то случайной погрешностью можно пренебречь и принять границы погрешности результата равными

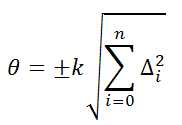
Если оба неравенства не выполняются, то границы погрешности результата измерений 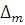приближенно можно представить в виде суммы 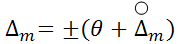. Результат многократного измерения физической величины 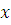записывают как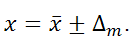

Пример.:

Результаты многократного измерения выходного напряжения стабилизатора (В) следующие: 220,0; 220,9; 219,9; 221,1; 221,3. Систематическая погрешность показаний составляет (+0,1 В). Доверительный интервал (доверительные границы по модулю ) для истинного значения силы с вероятностью Р=0,95 ( 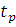=2,776) равен…

Решение:

1)Вносим поправку в каждое измерение

219.9; 220.8; 219.8; 221; 221.2

2) Вычисляем среднее арифметическое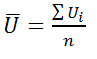

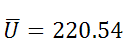
3) Вычисляем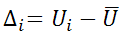

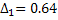
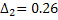
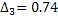
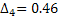
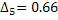
4) Вычисляем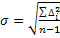

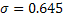, В

5) Вычисляем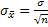

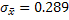, В

6) Находим границу погрешности случайного характера 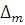(доверительный интервал при заданной доверительной вероятности Р=0,95

и соответствующем 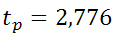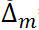=2,776 0,239=0,802 В

Поскольку НСП в данной задаче не учитывается, окончательный результат записывается в виде

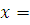220.54 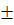0.802, В