Уравнение состояния идеального газа. (Уравнение Менделеева—Клапейрона.) Изопропессы

План ответа

1. Уравнение состояния. 2. Уравнение Менде­леева—Клапейрона. 3. Процессы в газах. 4. Изопроцессы. 5. Графики изопроцессов.

Состояние данной массы полностью определе­но, если известны давление, температура и объем га­за. Эти величины называютпараметрами состояния газа. Уравнение, связывающее параметры состояния, называютуравнением состояния.

Для произвольной массы газа единичное со­стояние газа описывается уравнением Менделеева— Клапейрона: pV = mRT/M, где р — давление, V —

объем, т — масса, М — молярная масса, R — уни­версальная газовая постоянная. Физический смысл универсальной газовой постоянной в том, что она по­казывает, какую работу совершает один моль иде­ального газа при изобарном расширении при нагре­вании на 1 К (R = 8,31 Дж/моль • К).

Уравнение Менделеева—Клапейрона показы­вает, что возможно одновременно изменение пяти параметров, характеризующих состояние идеального

газа. Однако многие процессы в газах, происходящие в природе и осуществляемые в технике, можно рас­сматривать приближенно как процессы, в которых изменяются лишь два параметра из пяти. Особую роль в физике и технике играют три процесса: изо­термический, изохорический и изобарный.

Изопроцессом называют процесс, происходя­щий с данной массой газа при одном постоянном па­раметре — температуре, давлении или объеме. Из уравнения состояния как частные случаи получаются законы для изопроцессов.

Изотермическим называют процесс, проте­кающий при постоянной температуре. Т = const. Он описывается законом Бойля-Мариотта. pV = const.

Изохорным называют процесс, протекающий при постоянном объеме. Для него справедлив закон Шарля. V = const. p/T = const.

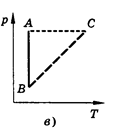
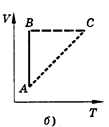
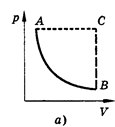Изобарным называют процесс, протекающий при постоянном давлении. Уравнение этого процесса имеет вид V/T == const при р = const и называется за­коном Гей-Люссака. Все процессы можно изобразить графически (рис. 11).

рис.11

Реальные газы удовлетворяют уравнению со­стояния идеального газа при не слишком высоких давлениях (пока собственный объем молекул прене­брежительно мал по сравнению с объемом сосуда, в котором находится газ) и при не слишком низких температурах (пока потенциальной энергией межмо­лекулярного взаимодействия можно пренебречь по сравнению с кинетической энергией теплового дви­жения молекул), т. е. для реального газа это уравнение и его следствия являются хорошим приближением.

Билет №11