Методические указания к выполнению
Контрольных заданий и практических работ
Эти указания реализованы в виде решения ряда характерных примеров с иллюстрацией хода решения, используемых справочных данных, порядка и способа представления полученных результатов. Рекомендуется ознакомиться с этими примерами до выполнения практических и контрольных работ.
Пример 1. Смесь идеальных газов задана объемными долями: 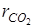 =0,6;
=0,6; 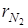 =0,3;
=0,3; 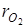 =0,1. Общая масса смеси mсм=20 кг. В начальном состоянии объем смеси V1=15 м3 и температура t1=47˚C. В результате адиабатного сжатия давление смеси увеличивается до p2=0,9 МПа.
=0,1. Общая масса смеси mсм=20 кг. В начальном состоянии объем смеси V1=15 м3 и температура t1=47˚C. В результате адиабатного сжатия давление смеси увеличивается до p2=0,9 МПа.
Определить давление смеси p1 в начальном состоянии, температуру t2 и объем V2 смеси в конечном состоянии, работу сжатия L1-2 и изменение внутренней энергии ΔU. Считать, что теплоемкость газов не зависит от температуры и определяется из приложения [П.1].
Определить парциальные давления газов, входящих в смесь, в конечном состоянии. Изобразить процесс в pv - и Ts - диаграммах.
Решение
Дано: V1, mсм, p2, t1, 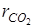 ,
, 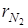 ,
, 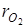 .
.
Необходимо найти: p1, t2, V2, L1-2, ΔU=U2–U1.
1. Сначала схематично представим рассматриваемый процесс в pv - и Ts - диаграммах, следуя рис. 4.1.
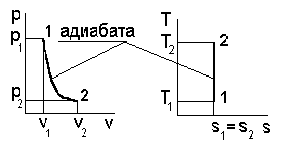
Рис. 4.1
2. Состояние исследуемой газовой смеси описывается уравнением Клапейрона - Менделеева (см. формулу 1), которое в обозначениях, принятых в данной задаче, можно представить в виде
p·V=mсм·Rсм·T. (4.1)
Газовая смесь из состояния 1 переходит в состояние 2 по адиабате, поэтому параметры начального и конечного состояний смеси связаны с уравнениями (1.59, 1.60, 1.61). Применительно ко всему объему (Vi=mсм·vi) эти уравнения принимают вид
p1· 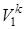 =p2·
=p2· 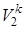 ; T1·
; T1· 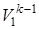 =T2·
=T2· 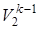 ; T1k·
; T1k· 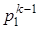 =T2k·
=T2k· 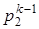 . (4.2)
. (4.2)
Из структуры формулы (4.1) следует, что, в начале необходимо определить газовую постоянную смеси Rсм. Для этого используем формулу (1.18):
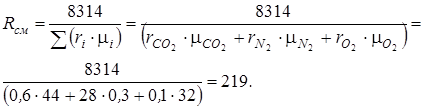
Анализ процесса сжатия смеси осуществляется при помощи уравнений (4.2), но прежде необходимо найти показатель адиабаты 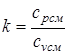 , для нахождения значения которого нужно рассчитать изобарную cpсм и изохорную cvсм теплоемкости смеси, используя формулы (1.22,1.21):
, для нахождения значения которого нужно рассчитать изобарную cpсм и изохорную cvсм теплоемкости смеси, используя формулы (1.22,1.21):

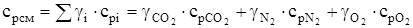
. (4.3)
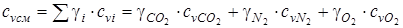
По условию рассматриваемой задачи смесь задана объемными долями ri, а в формулах (4.3) состав смеси выражен в массовых долях γi. Перевод в массовые доли производим при помощи формулы (1.19):
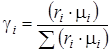 .
.
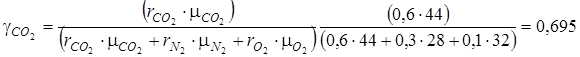 .
.
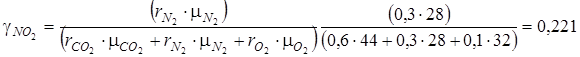 .
.
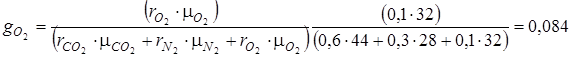 .
.
Из [П.1] находим значения мольных изобарных и изохорных теплоемкостей компонентов газовой смеси
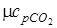 = 37,4;
= 37,4; 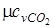 = 29,1
= 29,1
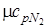 = 29,1 ;
= 29,1 ; 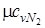 = 20,8
= 20,8
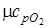 = 29,1 ;
= 29,1 ; 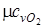 = 20,8
= 20,8
Переводим значения мольных теплоемкостей в массовые с помощью формул:
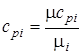 ;
; 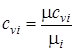
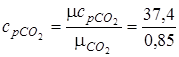 ;
;
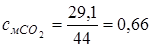 ;
;
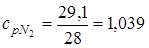 ;
;
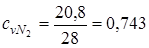 ;
;
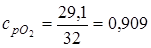 ;
;
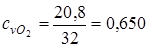 .
.
Найденные массовые доли компонентов газовой смеси γi и их изобарные, изохорные теплоемкости подставляем в уравнения (4.3):
cpсм=0,695·0,85+0,221·1,039+0,084·0,909=0,8967.
cvсм=0,695·0,66+0,221·1,743+0,084·0,650=0,6775.
Определяем значение показателя адиабаты:
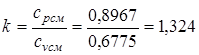 .
.
Формулу (4.1) напишем применительно к начальному состоянию смеси
р1V1=mсм ·R см ·T1,
где T1=t1+273.
Из последнего выражения находим начальное давление:
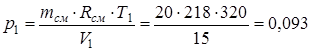 .
.
Далее в соответствии с первой из формул (4.2) p1 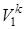 =p2
=p2 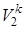 определяем конечный объем смеси:
определяем конечный объем смеси:
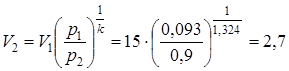 .
.
Пользуясь второй из формул (4.2) T1 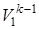 =T2
=T2 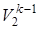 , рассчитываем конечную температуру смеси:
, рассчитываем конечную температуру смеси:
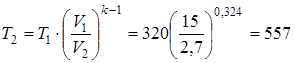 .
.
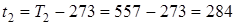 .
.
Обращаясь к формуле (1.63), находим удельную работу сжатия газовой смеси:
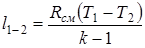 .
.
Применительно ко всей массе смеси работа сжатия равна
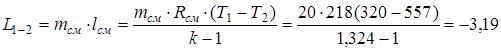 .
.
Отрицательное значение L1-2 означает, что эта работа внешних сил над газовой смесью.
Изменение удельной внутренней энергии смеси определяем, используя формулу (1.64)
Δu=(u2-u1)=cv·(T2-T1).
Применительно ко всей массе смеси изменение внутренней энергии равно
ΔU=U2-U1=mсм ·(u2-u1)=mсм ·cv·(T2-T1)=
=20·0,6775(557-320)=3,19.
Определяем парциальные давления компонентов газовой смеси. Из закона Бойля - Мариотта следует
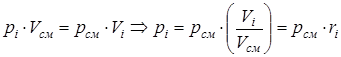 .
.
Используя последнее выражение, определяем парциальные давления компонентов газовой смеси:
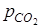 =
= 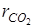 ·p2=0,6·0,9=0,54,
·p2=0,6·0,9=0,54,
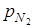 =
= 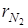 ·p2=0,3·0,9=0,27,
·p2=0,3·0,9=0,27,
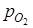 =
= 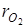 ·p2=0,1·0,9=0,09.
·p2=0,1·0,9=0,09.
Пример 2. Рассчитать цикл ДВС с изохорным подводом теплоты (цикл Отто), если начальные параметры рабочего тела p1=0,1 МПа, t1=20 ˚C, степень сжатия ε=6,5, а отведенная теплота |q2|=320 кДж/кг. Определить параметры состояния рабочего тела в характерных точках цикла, подведенное количество теплоты q1, работу цикла lц и термический КПД ηt, а также термический КПД цикла Карно в том же диапазоне температур. Изобразить цикл в координатах p, v и T, s. Рабочее тело - воздух. Средняя изохорная теплоемкость
cvm=0,716 кДж/(кг·К); удельная газовая постоянная Rв=287 Дж/(кг·К); показатель адиабаты k=1,4.
Решение
Дано: p1, t1,  , |q2|.
, |q2|.
Необходимо определить v1, v2, v3, v4, p2, p3, p4, t2, t3, t4, ηt, lц.
1. Представим рассматриваемый цикл в координатах p, v и T, s, следуя рис. 4.2.
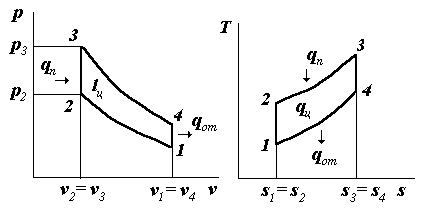
Рис. 4.2
Параметры точки 1: p1=0,1·106 Па; T1=273+t1=293 К.
Удельный объем определяем с помощью формулы (1.4).
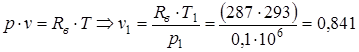 .
.
Параметры точки 2: находим, исследуя адиабатный процесс 1-2, который описывается формулой (1.59):
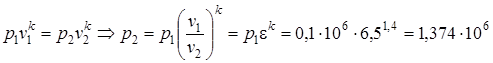 .
.
В соответствии с формулой (1.60)
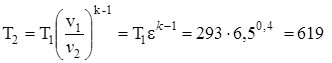 ,
,
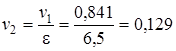 .
.
Для нахождения параметров точек 3, 4 составляем зависимости, соответствующие процессам: 2-3; 3-4; 4-1. Процесс 2-3 - изохорный, v3=v2=const. Из уравнения состояния pv=Rв·T следует 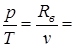 const. Следовательно,
const. Следовательно,
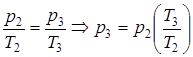 . (4.4)
. (4.4)
Для изохорного подвода теплоты справедлива зависимость
q1=сv·(T3-T2). (4.5)
Процесс 3-4 - адиабатный:
p3 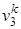 =p4
=p4 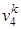 . (4.6)
. (4.6)
Процесс 4-1 - изохорный:
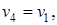
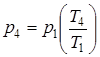 ; (4.7)
; (4.7)
и изохорный отвод теплоты
q2=сv·(T4–T1). (4.8)
В уравнениях (4.4 – 4.8) неизвестными являются p3, T3, p4, T4, q1. Решая эту замкнутую систему уравнений, находим искомые величины:
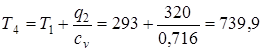 ,
,
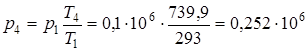 ,
,
p3= p4·εk=0,252·106·6,51,4=3,46·106,
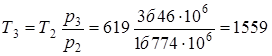 .
.
Параметры всех характерных точек найдены.
Находим количество подведенной теплоты в соответствии с формулами:
q1=cv(T3-T2)=0,716 (1559-619)=673 .
Определяем термический КПД по формуле (3.16):
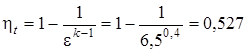 .
.
Рассчитываем работу цикла lц=q1-q2=(673-320)=353 кДж/кг.
Находим термический КПД цикла Карно в диапазоне температур
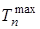 =T3=1559 K,
=T3=1559 K, 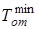 =T1=293 .
=T1=293 .
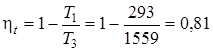 .
.
Пример 3. Из сужающегося сопла вытекает кислород, находящийся в резервуаре, давление и температура в котором р1=6 МПа, t1=100оС. Давление среды, в которую проходит истечение р2=3,6 МПа.
Определить скорость истечения и расход кислорода, если площадь выходного сечения f=20 мм2.
Газ подчиняется уравнению Клапейрона - Менделеева pv=RT, теплоемкость не зависит от температуры. Входная скорость кислорода близка к нулю. Процесс изменения состояния текущего газа изоэнтропный.
Решение. Прежде всего, устанавливаем каков режим истечения, для чего находим значение параметра 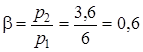 .
.
Сравниваем полученное значение с критическим отношением давлений в соответствии с формулой (2.56).
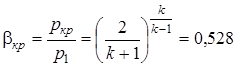 ,
,
где k=1,4 - коэффициент адиабаты;
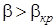 , т.е. это означает, что давление среды перед соплом больше, чем критическое, следовательно, располагаемый перепад давления будет использован полностью для разгона потока газа.
, т.е. это означает, что давление среды перед соплом больше, чем критическое, следовательно, располагаемый перепад давления будет использован полностью для разгона потока газа.
На выходе из сопла установится давление, равное давлению среды, а скорость истечения окажется меньше критической скорости, т.е. режим истечения будет - дозвуковой.
Определяем скорость истечения в соответствии с формулой (2.52):
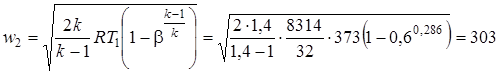 .
.
Подсчитываем удельный объем кислорода на выходе из сопла:
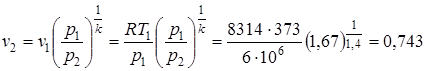 .
.
В заключение находим массовый расход кислорода при помощи уравнения неразрывности (2.40):
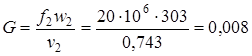 .
.
Пример 4. Необходимо определить конструктивные параметры сопла Лаваля, которое должно работать при следующих условиях.
На входе сопла давление и температура воздуха соответственно
р1=0,9 МПа, Т1=1100 К, в выходном сечении давление р2=0,11 МПа. Массовый расход газа G=0,7 кг/с.
Истечение через сопло адиабатное, при k=1,4. Трение газа в каннале и входная скорость его не учитываются. Удельная газовая постоянная
R=287 Дж/(кг∙К).
Решение. Находим отношение давлений в выходном сечении сопла:
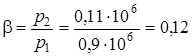 .
.
По формуле (2.56) определяем критическое значение 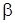 :
:
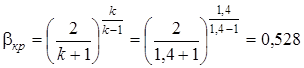 .
.
Для условий данного примера имеет место условие 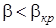 , следовательно, в минимальном сечении сопла будет достигнута критическая скорость и сопло Лаваля будет работать в сверхзвуковом режиме. Критическую скорость, соответствующую начальной температуре Т1=1100 К, определяем по формуле (2.57)
, следовательно, в минимальном сечении сопла будет достигнута критическая скорость и сопло Лаваля будет работать в сверхзвуковом режиме. Критическую скорость, соответствующую начальной температуре Т1=1100 К, определяем по формуле (2.57)
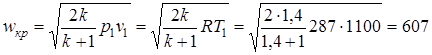 .
.
Площадь минимального сечения сопла находим по формуле:
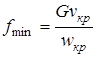 ,
,
где 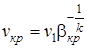 ;
; 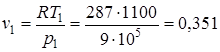 .
.
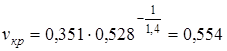 м3/кг;
м3/кг; 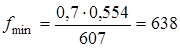 .
.
Диаметр минимального сечения сопла
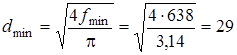 .
.
Длину сужающейся части сопла l1 обычно принимают равной диаметру минимального сечения:
l1=29.
Скорость газов в выходном сечении сопла находим по формуле (2.52):
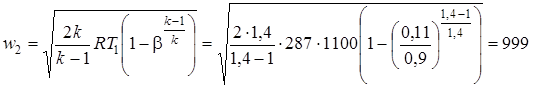 .
.
Площадь выходного сечения сопла находим по формуле
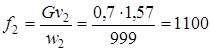 ,
,
где 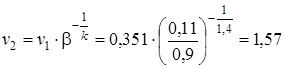 м3/кг.
м3/кг.
Диаметр выходного сечения будет равен
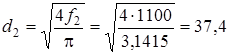 .
.
Длину расходящейся части сопла l2 находим по формуле (2.60), приняв угол конусности равным 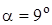 .
.
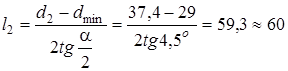 .
.
Пример 5. Определите состояние пара за турбиной и подсчитайте внутренний КПД паротурбинной установки, если начальные параметры р1=13,0 МПа и t1=565 °С, давление в конденсаторе р2=40 гПа, внутренние относительные КПД турбины и питательного насоса соответственно 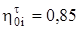 и
и 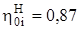 .
.
Решение. Цикл, по которому работает установка, изображен на рис. 35.
Сначала определим состояние пара в конце изоэнтропного расширения пара в турбине. Начальную энтальпию и энтропию находим по таблицам [7]:
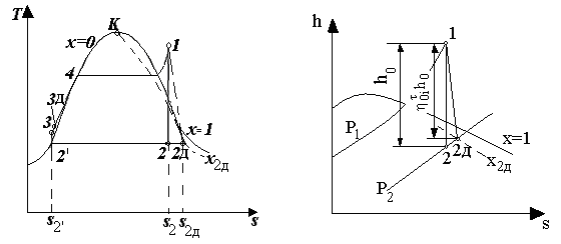
а б
Рис. 4.3
Для р1 = 13,0 МПа и t1 = 565 °С, 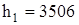 кДж/кг и
кДж/кг и 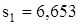 кДж/(кг·К). Для р2 = 40 гПа: определяем
кДж/(кг·К). Для р2 = 40 гПа: определяем 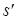 = 0,4225 кДж/(кг·К),
= 0,4225 кДж/(кг·К), 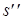 = 8,473 кДж/(кг·К), r = 2433 кДж/(кг·К),
= 8,473 кДж/(кг·К), r = 2433 кДж/(кг·К), 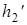 =121 кДж/(кг·К). Энтальпию пара в точке 2 находим, рассчитывая изоэнтропный процесс 1-2:
=121 кДж/(кг·К). Энтальпию пара в точке 2 находим, рассчитывая изоэнтропный процесс 1-2:
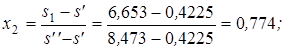
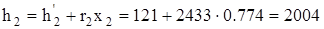 кДж/кг.
кДж/кг.
Таким образом, изоэнтропный теплоперепад
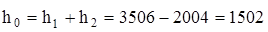 кДж/кг.
кДж/кг.
По определению
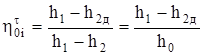
Следовательно,
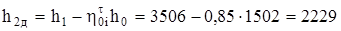 кДж/кг.
кДж/кг.
Зная энтальпию, легко найти остальные параметры при р2=40 гПа. Для этого сначала необходимо найти степень сухости в конце действительного процесса расширения:
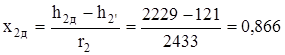 .
.
Внутренний КПД цикла определяется по формуле
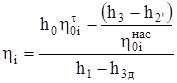
Находим энтальпию воды после теоретического и действительного (с учетом потерь) сжатия в насосе. Энтальпия 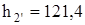 кДж/кг, энтропия
кДж/кг, энтропия 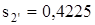 кДж/(кг·К). Энтальпия в точке 3 определяется в результате изоэнтропного процесса 2-3 (
кДж/(кг·К). Энтальпия в точке 3 определяется в результате изоэнтропного процесса 2-3 ( 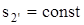 ). Интерполируя табличные данные [7], находим при давлении р3=р1=13,0 МПа и s3=0,4225 кДж/(кг·К) энтальпию h3=134,8 кДж/кг. Разность h3-h2’=134,8-121,4=13,4 кДж/кг представляет собой теоретическую работу насоса.
). Интерполируя табличные данные [7], находим при давлении р3=р1=13,0 МПа и s3=0,4225 кДж/(кг·К) энтальпию h3=134,8 кДж/кг. Разность h3-h2’=134,8-121,4=13,4 кДж/кг представляет собой теоретическую работу насоса.
Вычислим энтальпию в конце сжатия h3д с учетом потерь
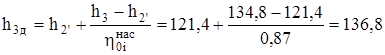 кДж/кг.
кДж/кг.
Таким образом,
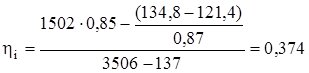 .
.
Определяем термический КПД цикла Ренкина (который не учитывает потери):
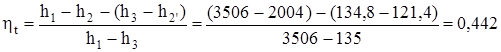 .
.
Если при определении внутреннего КПД установки пренебречь работой насоса, то окажется, что
 .
.
Здесь 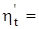
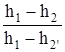 =
= 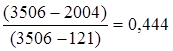 есть несколько завышенный термический КПД цикла не учитывающий работу насоса.
есть несколько завышенный термический КПД цикла не учитывающий работу насоса.
Разница 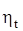 и
и 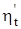 в нашем случае составляет 0,45 %. Приблизительно такой же будет ошибка и в определении расхода топлива. Тем не менее, соотношение
в нашем случае составляет 0,45 %. Приблизительно такой же будет ошибка и в определении расхода топлива. Тем не менее, соотношение
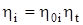
широко применяется в теплотехнических расчетах. Его можно считать вполне удовлетворительным при невысоких параметрах пара перед турбиной, когда работой насоса можно пренебрегать.
Пример 6. Паротурбинная установка, оснащенная теплообменниками смешивающего типа, работает по регенеративному циклу, имея два отбора при давлениях рm=1 МПа; рn=0,1 МПа. Турбина работает с начальными параметрами пара р1=5 МПа, t1=400oC, а давление в конденсаторе р2=5 кПа.
Определить термический КПД для регенеративного цикла Ренкина 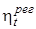 , удельный расход пара сравнить
, удельный расход пара сравнить 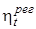 с КПД цикла Ренкина без регенеративного подогрева питательной воды.
с КПД цикла Ренкина без регенеративного подогрева питательной воды.
Решение
В соответствии с рис. 4.8, а также следуя рис. 4.9, для рассматриваемого цикла по hs - диаграмме находим h1=3192 кДж/кг; hm=2800 кДж/кг; hn=2408 кДж/кг; h2=2024 кДж/кг, по таблице состояния водяного пара [П.4] определяем: 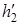 =138 кДж/кг;
=138 кДж/кг; 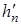 =417 кДж/кг;
=417 кДж/кг; 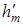 =763 кДж/кг.
=763 кДж/кг.
Величины отборов α1 и α2 вычисляем, используя формулы (4.31):
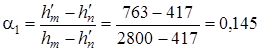 ;
;
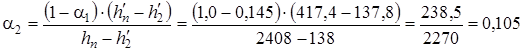 .
.
Определяем полезную работу, совершаемую 1 кг пара, по формуле (4.32)
lп=(h1-h2)-α1(hm-h2)-α2(hn-h2)=
=(3192-2024)-0,145(2800-2024)-0,105(2408-2024)=1015,2.
Удельная теплота, которая должна подводиться к 1 кг рабочего тела в паровом котле ПК и в парогенераторе ПП, определяется по формуле (4.34):
q1=(h1- 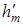 )=3192-763=2429.
)=3192-763=2429.
Термический КПД ПТУ с регенеративным циклом рассчитывается по формуле (4.35):
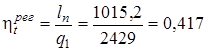 .
.
Термический КПД основного цикла Ренкина находим в соответствии с формулой (4.37):
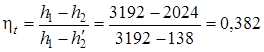 .
.
Увеличение термического КПД ПТУ составит
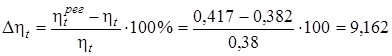 %.
%.
Определяем удельный расход пара по формуле (4.36):
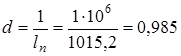 .
.
Пример 7. Воздушная холодильная машина производит лед при температуре - 3оС из воды с температурой 10 оС. Всасываемый в компрессор воздух имеет температуру t1=-10оС, давление р1=0,098 МПа и сжимается до давления р2=0,4 МПа. Затем воздух поступает в холодильник и там охлаждается до температуры t3=20оС. Расход воздуха равен Vо=1000 м3/чaс при нормальных условиях. После охладителя воздух попадает в детандер и расширяется перед поступлением в охлаждаемый объект.
Определить холодильный коэффициент ε, мощность, потребную для привода компрессора, и количество получаемого в час льда.
Решение
Схема воздушной холодильной установки и цикл ее работы представлены на рис. 4.4, а, б, в.
На рис. 4.4, а обозначены: 1 - охлаждаемый объект; 2 - компрессор; 3 - охладитель; 4 - детандер, где воздух адиабатно расширяется перед поступлением в охлаждаемый объект - 1.
На pv - и Ts - диаграммах (на рис. 4.4, б и в):
процесс 1-2 - адиабатное сжатие воздуха в компрессоре - 2;
процесс 2-3 - изобарное охлаждение с отводом теплоты q1 в охладителе - 3;
процесс 3-4 - адиабатное расширение воздуха в детандере - 4;
процесс 4-1 - изобарный отвод теплоты q2 в охлаждаемом объекте.
а б в
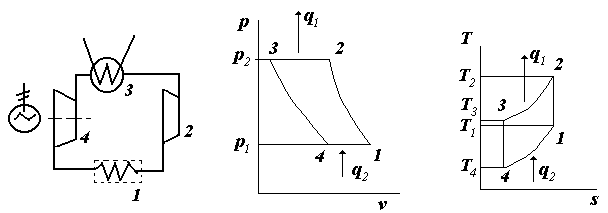
Рис. 4.4
1. Сначала определяем температуру воздуха в характерных точках цикла.
Анализ адиабатного процесса 1-2 позволяет вычислить температуру сжатого в компрессоре 2 воздуха:
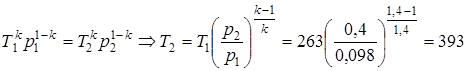 ,
,
где Т1=t1+273, k=1,4 - коэффициент адиабаты для воздуха.
Определяем температуру воздуха после его расширения в детандере 4, для чего анализируем адиабатный процесс 3-4:
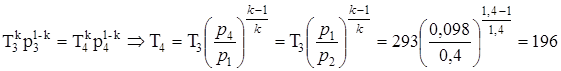 ,
,
где Т3=t3+273.
2. Определяем холодильный коэффициент холодильной установки.
Для этого используем формулу (5.2):
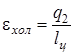 ,
,
где q2 - количество удельной отводимой теплоты от охлаждаемого тела;
lц - работа, затраченная на это.
Процесс 4-1 - изобарный, поэтому отводимая теплота определится по формуле
q2=cp(T1-T4).
Находим теплоту, отнимаемую от воздуха в охладителе 3, в соответствии с изобарным процессом 2-3:
q1=cp(T2-T3).
Работа цикла определяется как разность соответствующих теплот:
lц=q1-q2=cp(T2-T3)-cp(T1-T4).
Тогда холодильный коэффициент равен
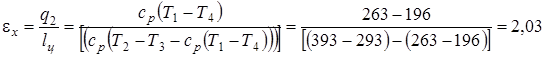 .
.
3. Определяем количество теплоты, отнимаемое от воды при образовании 1 кг льда, которое состоит из следующих составляющих:
а) теплота, идущая на охлаждение воды от 10оС до 0оС:
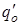 =
= 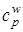 (t2-t1)=4,187(10-0)=41,87;
(t2-t1)=4,187(10-0)=41,87;
б) теплота плавления льда
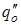 =330,7 [9];
=330,7 [9];
в) теплота, которая должна отводиться при понижении температуры льда от 0оС до -3оС
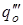 =cл(t1-t2)=2,09[0-0(-3)]=6,27,
=cл(t1-t2)=2,09[0-0(-3)]=6,27,
где 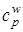 и сл - соответственно теплоемкость воды и льда.
и сл - соответственно теплоемкость воды и льда.
Общее количество теплоты, которое отнимается при образовании 1 кг льда
qo= 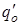 +
+ 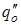 +
+ 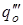 =41,87+330,70+6,27=378,74 .
=41,87+330,70+6,27=378,74 .
4. Определяем хладопроизводительность установки Qо, которая равна количеству теплоты, отводимому в единицу времени от охлаждаемого объекта.
Сначала вычисляем часовой массовый расход воздуха - mo, через компрессор:
mo=Vo(м3/час)∙ρ(кг/м3)=1000∙1,298=1298,
где 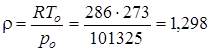 кг/м3 - плотность воздуха при нормальных условиях.
кг/м3 - плотность воздуха при нормальных условиях.
В соответствии с изобарным процессом 4-1 количество отводимой теплоты определяется по формуле
Qo=moq2=mocp(T1-T4)=1298∙1006(263-196)=87,96,
где ср - теплоемкость воздуха.
Количество получаемого в холодильнике льда будет равно
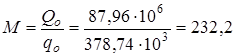 .
.
Используя формулу (5.2) применительно ко всему потоку воздуха, прокачиваемого через компрессор, находим работу
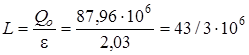 .
.
Дата добавления: 2021-07-22; просмотров: 592;











