ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Дросселирование – это течение газа через гидравлические сопротивления, в которых частично теряется его кинетическая энергия. При движении газа без теплообмена с окружающей средой через пористый материал (рис. 4), представляющий собой систему мельчайших каналов, его давление р понижается, а энтальпия h = u + pv остается постоянной. Это явление названо «эффектом Джоуля-Томсона», по фамилиям исследовавших его ученых. В идеальном газе температура при течении через пористую перегородку остается постоянной. В реальном газе вследствие межмолекулярного взаимодействия температура меняется.

В «идеальном газе» размеры молекул считаются пренебрежимо – малыми и силы взаимодействия между ними отсутствуют. Параметры состояния идеального газа связаны уравнением Клапейрона-Менделеева:

pv = RT, (8)

где р – давление;

v – удельный объем;

Т – абсолютная температура;

R – газовая постоянная удельная.

Для реального газа связь между параметрами сложнее. Одно из относительно простых уравнений, описывающих эту связь, предложено Ван-дер-Ваальсом:

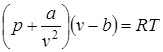, (9)

где b – поправка на объем, занимаемый молекулами;

- поправка на силы взаимодействия между молекулами.

Если при бесконечно малом изменении давления происходит бесконечно малое изменение температуры, то можно написать

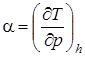или (10)

где индекс h означает изменение параметров в процессе при h=const.

Величина 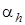называется дифференциальным дроссель-эффектом Джоуля-Томсона. Так как всегда 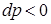, то при положительном значении 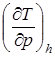температура газа понижается , при отрицательном значении-температура газа возрастает 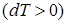, а при температура газа неизменна .

Состояние газа, при котором , называется точкой инверсии эффекта Джоуля-Томсона, а температура при этом состоянии –температурой инверсии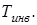

Значение 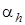определяется из уравнения

(11)

Так как при дросселировании , то из (11) следует

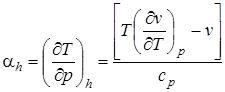(12)

Полагая, что реальный газ является Ван-дер-Ваальсовским газом

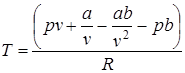(13)

Продифференцируем уравнение (13) при p=const и подставив это выражение в уравнение (12) после приведения к общему знаменателю получим

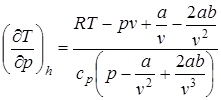(14)

В уравнении (14) коэффициенты a и b, зависящие от параметров критической точки данного газа, определяются по формулам:

;

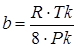
Таким образом, по уравнениям (13) и (14) можно определить значения 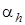при заданном давлении 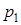. Для этого, задаваясь различными значениями удельного объема v, по (13) вычисляют соответствующие им температуры, затем, подставляя v и T в (14) находят значение дифференциального дроссель эффекта .

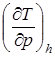Отклонение процесса дросселирования реальных газов от идеального связаны с размерами молекул (молекулярной массой) и с параметрами состояния. При этом «дроссель-эффект», т.е. изменение температуры, может быть положительным (Т₁ > Т₂), отрицательным (Т₁ < Т₂) и нулевым (Т₁ = Т₂).

При дросселировании газа увеличивается его энтропия. Реальные процессы движения газов и паров в трубопроводах, арматуре, в лопаточных решетках турбомашин всегда сопровождаются дросселированием из-за вязкого трения и поэтому являются необратимыми.

Понижение температуры реального газа при дросселировании используется в технике для получения низких температур и сжижения газов.