Квантовые эффекты в полупроводниках

В начале 70-х гг. прошлого века в физике полупроводников появилось новое направление — изучение гетероструктур, образованных различными по своему составу и свойствам полупроводниками. В особенности интересными оказались гетероструктуры, в которых пространственная размерность отлича­ется от трехмерной, т.е. от обычного твердого тела. Это могут быть тонкие пленки нанометровой толщины, такой же толщины тонкие нити и нанометровые ансамбли атомов. Поскольку на нанометровых размерах проявляются квантовые эффекты, эти системы были названы квантовыми ямами, квантовы­ми нитями и квантовыми точками. Их замечательная особенность заключается в том, что наноразмеры полупроводниковых структур ограничивают движение электронов и поэтому плотность электронных состояний в нихпринципиально отличается от макроскопического тела. Нетрудно видеть (рис 11,3), что кван­товые эффекты проявляются, начиная с квантовых ям, т. е. когда движение электронов ограничено нанометровыми размерами, хотя бы в одном измерении.

Рис. 4.27.Плотность энергетических состояний для трехмерного твердого тела-1,

квантовой ямы-2, нити-3, точки-4.

Не останавливаясь на интереснейших свойствах и практических приложе­ниях квантовых ям и квантовых нитей, поговорим о квантовых точках, которые рассматриваются сегодня как одна из возможных альтернатив молекулярной элементной базе вычислительных устройств.

Квантовые точки называют иногда, чаще в популярных изданиях, искус­ственными атомами. Но квантовая точка – это совокупность атомов с на-норазмерами по всем трем пространственным измерениям. Движение элек­тронов в такой системе может быть аппроксимировано простейшей квантово механической моделью, известной под названием «частица в прямоугольном потенциальном поле». Эта модель описывается уравнением Шредингера

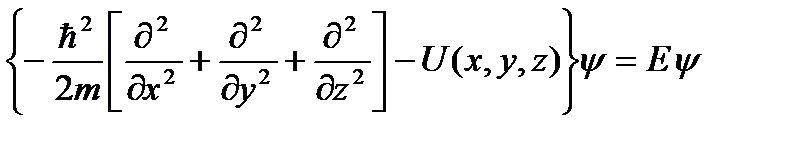, (4.11)

где потенциальная энергия в ящике со сторонами a, b, c

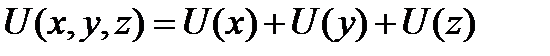. (4.12)

При этом

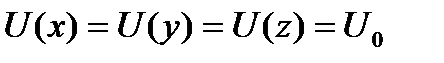при всех других значениях x, y, z.

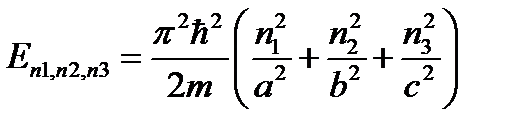, где n1, n2, n3=1,2,3,... (4.13)

Таким образом, квантовой точке отвечает дискретный спектр, сходный по общему виду со спектром атомной системы.

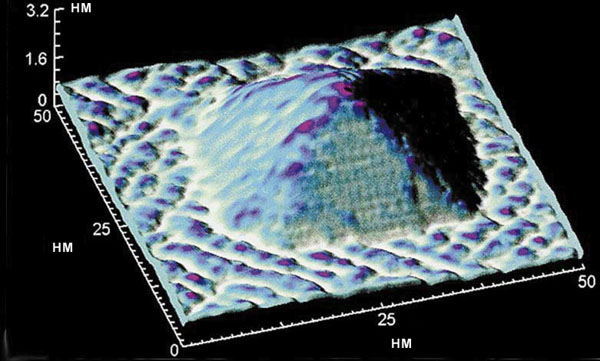
Рис. 4.28.Экспериментальная полупроводниковая реализация квантовой точки

В квантовой точке могут находиться от одного до большого количества электронов, распределение которых определяется принципом Паули.

Квантовые точки могут быть созданы методом молекулярно-лучевой эпитаксии. На хорошо подготовленную поверхность напыляется другое вещество со структурой, близкой к структуре подложки. При этом все должно происхо­дить в высоком вакууме, чтобы избежать включения в формируемый объект посторонних примесей. Скорость напыления должна тщательно регулироваться для того, чтобы исключить образование дефектов структуры. Спонтанное фор­мирование квантовых точек в так называемом режиме Странского-Крастанова хорошо изучено на примере системы InAs/GaAs. При росте первого моно­молекулярного слоя InAs на поверхности GaAs из-за различия постоянных кристаллических решеток возникают упругие напряжения. Если напыление продолжается, они увеличиваются, и становится выгодным не равномерное распределение вещества по поверхности первого слоя, а образование отдель­ных «капель» на поверхности первого слоя (его называют «смачивающим» слоем). Таким образом, возникают «пирамидки» со свойствами квантовых точек (рис. 4.28).

Рис. 4.29. Зонная структура полупроводника, содержащего квантовую точку

Качественно эти пирамидки можно рассматривать как дефекты на поверх­ности основного полупроводника. В этом случае в зонной структуре появля­ются примесные уровни (рис. 4.29) – несколько выше валентной зоны (дырки) и несколько ниже зоны проводимости (электроны). Уровни, отвечающие при­месному уровню зоны проводимости, характеризуются дискретным спектром, т.е. они отвечают квантовой точке.