Уравнение процесса дросселирования

Дросселированием называется необратимый процесс протекания газа (пара) через местное сопротивление, в результате которого снижается давление газа без совершения им технической работы.

Местное сопротивление потоку создают установленные в трубопроводе вентиль, задвижка, кран, клапан, диафрагма, пористая перегородка, капиллярная трубка и другие устройства.

Рассмотрим адиабатное (без теплообмена с окружающей средой) течение газа по трубопроводу через местное сопротивление, создаваемое, например, диафрагмой (рис. 2.15).

При подходе к диафрагме поток, сужаясь, разгоняется, давление внутри его уменьшается, а на стенки трубопровода и диафрагмы вследствие торможения газа в застойной зоне оно несколько повышается. После прохождения отверстия поток, расширяясь до стенок трубопровода, тормозится, давление газа при этом возрастает. Однако давление р₂ в сечении II после диафрагмы оказывается меньше давления р₁ в сечении I перед диафрагмой. Снижение давления является следствием потерь на трение и вихреобразование, вызванное разностью давлений у стенок диафрагмы и в потоке. Вследствие этих потерь процесс дросселирования является необратимым процессом и протекает с увеличением энтропии.

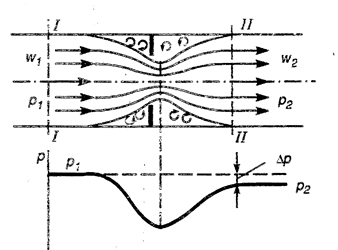
Рис. 2.15. Изменение давления при

дросселировании газа диафрагмой

Величина снижения давления зависит от природы газа, параметров его состояния, скорости движения и степени сужения трубопровода.

После дросселирования удельный объем и скорость газа возрастают (v₂ > v₁ и w₂ > w₁), а температура газа в зависимости от его природы и параметров состояния перед дросселированием может как увеличиваться, так и уменьшаться, или оставаться неизменной.

Изменение температуры после дросселирования газа и пара, открытое Джоулем и Томсоном в 1852г., называется дроссель-эффектом Джоуля – Томсона.

Для адиабатного процесса дросселирования справедливо уравнение

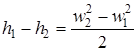. (2.66)

При неизменном диаметре трубы (F = const) и стационарном процессе, в котором через любое сечение массовый расход газа G = const, в соответствии с уравнением неразрывности (2.33)

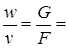const. (2.67)

Отсюда следует, что скорость газа возрастает пропорционально увеличению объема. Однако при таком изменении скорости изменение кинетической энергии газа в сравнении с величиной его энтальпии оказывается ничтожно малым. Таким образом, изменением кинетической энергии газа при дросселировании можно пренебречь, тогда

h₁ =h₂, или u₁ + p₁v₁ = u₂ + p₂v₂.

Для идеального газа энтальпия является однозначной функцией температуры, поэтому эффект Джоуля –Томсона для него равен нулю.

В отличие от идеального в реальном газе имеются силы притяжения между молекулами и при расширении его внутренняя потенциальная энергия возрастает. Это и является причиной возможного изменения температуры реального газа при дросселировании. Если при бесконечно малом изменении давления происходит бесконечно малое изменение температуры, то можно написать

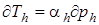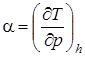или , (2.68)

где индекс «h» означает изменение параметров в процессе при h = const.

Величина 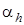называется дифференциальным дроссель –эффектом Джоуля –Томсона. Так как всегда dp < 0, то при положительном значении 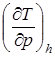температура газа понижается (dT < 0), при отрицательном значении –температура газа возрастает (dT > 0), а при 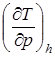=0 температура газа неизменна (dT = 0).

Состояние газа, при котором 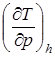=0, называется точкой инверсии эффекта Джоуля –Томсона, а температура при этом состоянии –температурой инверсии Т_инв .

Значение 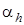определяется из уравнения

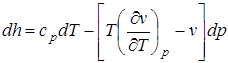(2.69)

вывод которого дается в литературе, содержащей рассмотрение дифференциальных уравнений термодинамики [1, 3].

Так как при дросселировании dh = 0, то из (2.69) следует

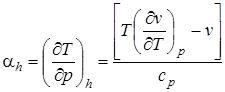. (2.70)

Полагая, что реальный газ является Ван –дер –Ваальсовским газом

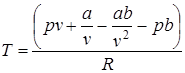. (2.71)

Продифференцируем уравнение (2.71) при p = const:

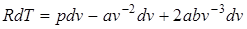
Отсюда .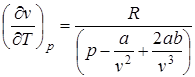

Подставив это выражение в уравнение (2.70), после приведения к общему знаменателю получим

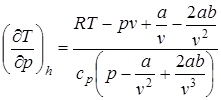. (2.72)

В уравнении (2.72) коэффициенты a и b, зависящие от параметров критической точки данного газа, определяются в работе [1].

Для идеального газа а=0 и b=0 и уравнение (2.72) дает .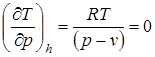

Таким образом, по уравнениям (2.71) и (2.72) можно определить значение 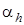при заданном давлении р₁. Для этого, задаваясь различными значениями удельного объема v, по (2.71) вычисляют соответствующие им температуры, затем, подставляя v и T в (2.72), находят значение дифференциального дроссель эффекта .

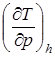Температуры, при которых кривые пересекают ось абсцисс, являются температурами инверсии. Перенеся значение температур при различных давлениях в рТ –координаты, получим кривую l инверсии (рис. 2.16), в каждой точке которой дроссель –эффект равен нулю и температура газа при дросселировании не изменяется. Точки на поле диаграммы внутри кривой соответствуют охлаждению газа, а снаружи кривой –подогреву газа. На этом же рисунке дана экспериментальная кривая 2-инверсия воздуха. Ее расхождение с теоретической кривой объясняется тем, что уравнение Ван –дер –Ваальса лишь приближенно отражает реальную связь параметров состояния воздуха.

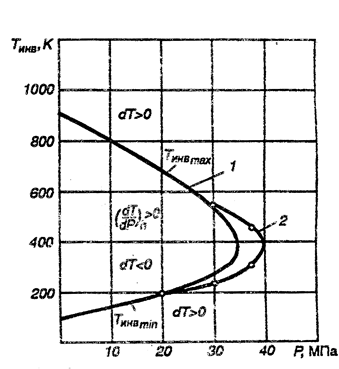
Рис. 2.16. Инверсионная кривая воздуха:

1 –расчетная; 2 –экспериментальная

Дифференциальный дроссель –эффект используется для определения температуры газа после дросселирования при малом уменьшении давления. При значительном снижении давления изменение температуры газа определяется интегральным дроссель –эффектом Джоуля –Томсона

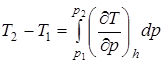. (2.73)

Практически интегрирование этого уравнения может быть выполнено по частям с учетом зависимости 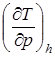от давления и температуры.

Процесс дросселирования, как было отмечено, является существенно необратимым процессом, протекающим с увеличением энтропии и снижением работоспособности рабочего тела. Тем не менее он находит применение в практике и создается искусственно в холодильных установках для понижения температуры, в приборах, измеряющих расход газа, в установках, сжижающих газ и в некоторых других устройствах.

Вопросы для самопроверки

1. Какие предпосылки положены в основу идеализации процесса адиабатного дросселирования?

2. На что затрачивается работа расширения при дросселировании?

3. Получите выражение для дифференциального дроссель –эффекта.

4. Изобразите кривую инверсии.

5. Сопоставьте температурный эффект охлаждения при обратимом адиабатном расширении и адиабатном дросселировании.

6. Покажите с помощью hs –диаграммы, как изменяется состояние водяного пара при дросселировании.

7. Как изменяются параметры идеального газа при дросселировании?